Test: Hamiltonian Paths & Circuits - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Hamiltonian Paths & Circuits
Identify true statements:
(I) Every complete graph is Hamiltonian
(II) Every wheel graph is Hamiltonian
(III) Every complete bipartite graph is Hamiltonian
(I) Every complete graph is Hamiltonian
(II) Every wheel graph is Hamiltonian
(III) Every complete bipartite graph is Hamiltonian
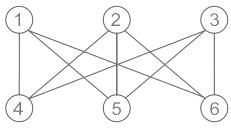
Consider the following graph:
Number of Hamiltonian Cycles starting and ending at A is _______

If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
For which values of m and n does the complete bipartite graph km, n have a Hamilton circuit?
If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
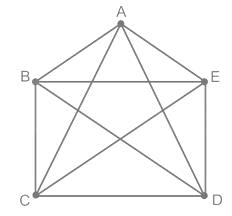
How many Hamiltonian paths does the following graph have?
What is the time complexity for finding a Hamiltonian path for a graph having N vertices (using permutation)?
Who invented the inclusion-exclusion principle to solve the Hamiltonian path problem?
In what time can the Hamiltonian path problem can be solved using dynamic programming?
Who formulated the first ever algorithm for solving the Hamiltonian path problem?