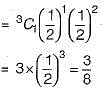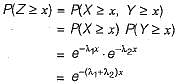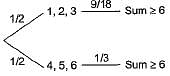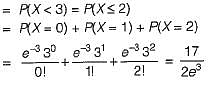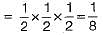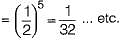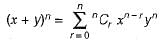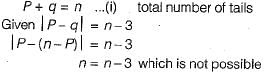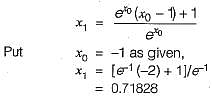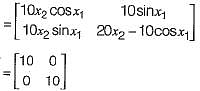Test: Probability- 2 - Civil Engineering (CE) MCQ
15 Questions MCQ Test Engineering Mathematics - Test: Probability- 2
A die is rolled three times. The probability that exactly one odd number turns up among the three outcomes is
Seven (distinct) car accidents occurred in a week. What is the probability that they all occurred on the same day?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let X and Y be two exponentially distributed and independent random variables with mean α and β, respectively. If Z= min (X, Y), then the mean of Z is given by
A bag contains 10 blue marbles, 20 green marbles and 30 red marbles. A marble is drawn from the bag, its colour recorded and it is put back in the bag. This process is repeated 3 times. The probability that no two of the marbles drawn have the same colour is
In a certain town, the probability that it will rain in the afternoon is known to be 0.6. Moreover, meteorological data indicates that if the temperature at noon is less than or equal to 250C, the probability that it will rain in the afternoon is 0.4. The temperature at noon is equally likely to be above 250C, or at/below 250C.
What is the probability that it will rain in the afternoon on a day when the temperature at noon is above 250C?
Suppose a fair six-sided die is rolled once, if the value on the die is 1, 2 or 3 then die is rolled a second time. What is the probability that the sum total of values that turn up is at least 6?
Suppose p is the number of cars per minute passing through a certain road junction between 5 PM and p has Poisson distribution with mean 3. What is the probability of observing fewer than 3 cars during any given minute in this interval?
A fair coin is tossed till a head appears for the first time. The probability that the number of required tosses is odd, is
A continuous random variable Xhas a probability density function f(x) = e-x, 0 < x <∝. Then P{X> 1} is
A fair coin is tossed n times. The probability that the difference between the number of heads and tails is ( n - 3) is
Two players, A and B, alternately keep rolling a fair dice. The person to get a six first wins the game. Given that player A starts the game, the probability that A wins the game is
Equation ex - 1 = 0 is required to be solved using Newton's method with an initial guess x0 = -1. Then, after one step of Newton’s method, estimate x1 of the solution will be given by
Let x2 - 117 = 0. The iterative steps for the solution using Newton-Raphson’s method is given by
Solution of the variables x1 and x2 for the following equations is to be obtained by employing the Newton-Raphson iterative method
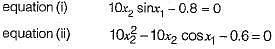
Assuming the initial values x1 = 0.0 and x2 = 1.0, the Jacobian matrix is
When the Newton-Raphson method is applied to solve the equation f(x) = x3 + 2x - 1 = 0, the solution at the end of the first iteration with the initial guess value as x0 = 1.2 is
|
65 videos|120 docs|94 tests
|
|
65 videos|120 docs|94 tests
|