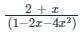Test: Recurrence Relations - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Recurrence Relations
Consider the recurrence relation a1=4, an=5n+an-1. The value of a64 is _________
What is the recurrence relation for 1, 7, 31, 127, 499?
Solution to recurrence relation T(n) = T(n - 1) + 2 is given by, where n > 0 and T(0) = 5.
Find the generating function for the sequence given recursively by
an - 2an-1 - 4an-2 = 0 with a0 = 2 and a1 = 5?
Find the value of a4 for the recurrence relation an = 2an-1 + 3, with a0 = 6.
Determine the solution for the recurrence relation bn = 8bn-1 − 12bn-2 with b0 = 3 and b1 = 4.
Determine the value of a2 for the recurrence relation an = 17an-1 + 30n with a0 = 3.
Determine the solution of the recurrence relation Fn = 20Fn-1 − 25Fn-2 where F0 = 4 and F1 = 14.
If Sn = 4Sn-1 + 12n, where S0 = 6 and S1 = 7, find the solution for the recurrence relation.
The solution to the recurrence relation an = an-1 + 2n, with initial term a0 = 2 are _________