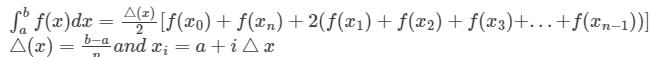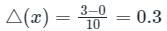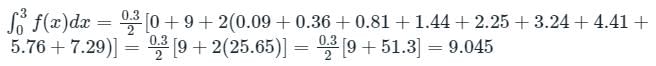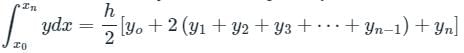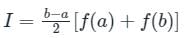Test: Trapezoidal Rule - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Trapezoidal Rule
Which order of Polynomials can best be integrated using Trapezoidal Rules?
P(0,3), Q(0.5,4) and R(1,5) are three points on the curve defined by f(x). Numerical integration is carried out using both trapezoidal rule and simpson’s rule within limits x = 0 and x = 1 for the curve. The difference between the two results will be
Function f is known at the following points:

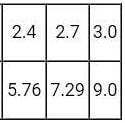
The value 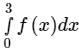 computed using the trapezoidal rule is
computed using the trapezoidal rule is
The error in numerically computing the integral 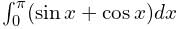 sing the trapezoidal rule with three intervals of equal length between 0 and π is
sing the trapezoidal rule with three intervals of equal length between 0 and π is
The area under a straight line is an estimate of the integral of f(x) between the limits a and b and the result of this integration is called the trapezoidal rule. The formula used in area calculation by this rule is
Which of the following indicates the assumption assumed in the trapezoidal formula?
Numerical integration using trapezoidal rule gives the best result for a single variable function, which is
Calculate the volume of third section, if the areas are 76.32 sq. m and 24.56 sq. m with are at a distance of 4 m.




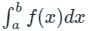 is given by
is given by