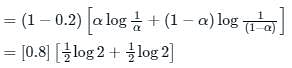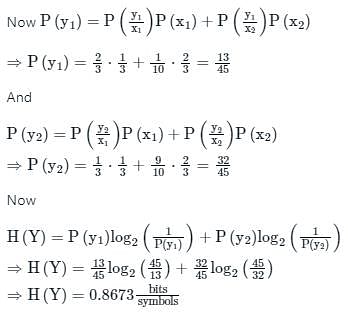Test: Mutual Information - Electronics and Communication Engineering (ECE) MCQ
8 Questions MCQ Test Communication System - Test: Mutual Information
Read the following expression regarding mutual information I(X;Y). Which of the following expressions is/are correct
Which of the following statements are correct?
(A) A given source will have maximum entropy if the produced are statistically independent
(B) As the bandwidth approaches infinity, the channel capacity becomes zero.
(C) For binary transmission the baud rate is always equal to bit rate
(D) The mutual information of a channel with independent input and output is constant
(E) Nat is a unit of information
Choose the correct answer from the options given below:
(1) (A) and (E) only
(2) (A) and (B) only
(3) (C) and (E) only
(4) (A), (D) and (E) only
(A) A given source will have maximum entropy if the produced are statistically independent
(B) As the bandwidth approaches infinity, the channel capacity becomes zero.
(C) For binary transmission the baud rate is always equal to bit rate
(D) The mutual information of a channel with independent input and output is constant
(E) Nat is a unit of information
Choose the correct answer from the options given below:
(1) (A) and (E) only
(2) (A) and (B) only
(3) (C) and (E) only
(4) (A), (D) and (E) only
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let (X1, X2) be independent random varibales. X1 has mean 0 and variance 1, while X2 has mean 1 and variance 4. The mutual information I(X1 ; X2) between X1 and X2 in bits is_______.
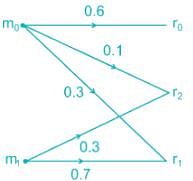
For the channel shown below if the source generates two symbols m0 and m1 with a probability of 0.6 and 0.4 respectively. The probability of error if the receiver uses MAP coding will be_______(correct up to two decimal places)
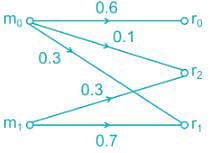
For the channel shown below, if the source generates M0 and M1 symbols. The probability of error using ML decoding is
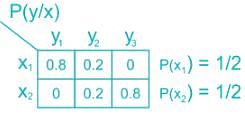
Consider a Binary - channel
P(x1) = 0.5
P(x2) = 0.5

Find the mutual Information in bits/symbol
In data communication using error detection code, as soon as an error is detected, an automatic request for retransmission (ARQ) enables retransmission of data. such binary erasure channel can be modeled as shown:
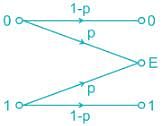
If P = 0.2 and both symbols are generated with equal probability. Then mutual information I(x, y) is _______.
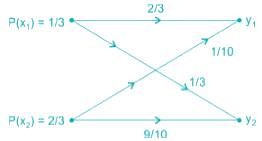
A binary channel matrix is given by
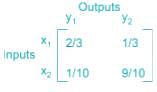
Given, P(x1) = 1/3 and P(x2) = 2/3. The value of H(Y) is ________bit/symbol.
|
14 videos|38 docs|30 tests
|
|
14 videos|38 docs|30 tests
|