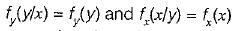Test: Theory of Random Variable & Noise - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Theory of Random Variable & Noise
A certain random variable has the CDF (cumulative distribution function) given by:
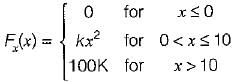
Which of the following options is/are not correct?
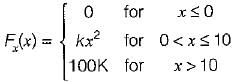
Which of the following options is/are not correct?
A radio receiver with 10 kHz bandwidth has a noise figure of 30 dB. The noise power at input is (take K = 1.38 x 10-23 J/Kelvin and assume room temperature of 300 K)
The probability density function of a random variable is given by
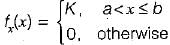
The value of constant K is
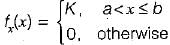
The value of constant K is
Consider the following statements associated with different types of noise occurring in nature:
1. The flicker noise occurs at high operating frequencies (few MHz).
2. Shot noise is produced due to random variations in the arrival of electrons at the output electrode of an amplifying device.
3. The thermal noise is proportional to temperature and the value of the resistance and is independent of bandwidth.
4. Noise can also be represented by fictitious temperature called noise temperature.
Which of the statements given above is/are not correct?
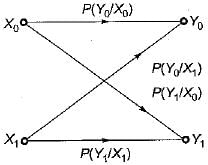
Over a certain binary communication channel (BCC), symbol ‘O' is transmitted with a probability of 0.4 and symbol ‘1’ is transmitted with a probability of 0.6. The probability of error when '1' is transmitted is 10-4 and that when a ‘0' is transmitted is 10-6.
What is the probability of error in the channel?
The joint PDF of the.random variable x and y is given by,
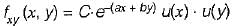
where, a and b are constants. The value of C is
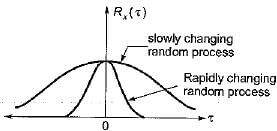
Assertion (A): if the random process x(t) changes very rapidly with time, the autocorrelation function will decrease rapidly to zero.
Reason (R): The autocorrelation function Rx(τ) is a measure of interdependence of two random variables obtained by observing the random process x(t) at time τ seconds apart.
Consider the following statements associated with conditional probability density function (PDF):
1. The conditional PDF is basically a probability, density function (PDF).
2. The conditional PDF is a non-negative function.
3. The area under a conditional PDF is always equal to 1,
4. The conditional density functions reduce to the marginal density functions.
Which of the statements given above are correct?
The distribution function of random variable is


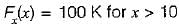
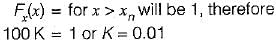
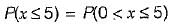
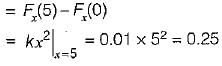
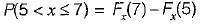
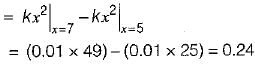
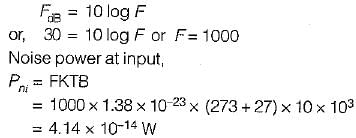

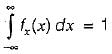
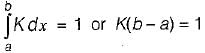
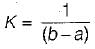
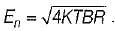
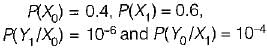
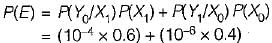
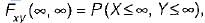 which will be equal to 1 because the probability of
which will be equal to 1 because the probability of 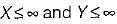 covers all the possible values of random variables X and Y.
covers all the possible values of random variables X and Y.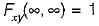
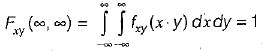
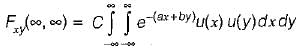
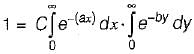
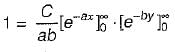
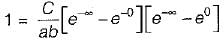
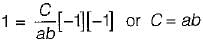
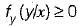 i.e. the conditional PDF is a non negative function.
i.e. the conditional PDF is a non negative function.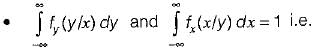 th e area under a conditional PDF is always equal to 1. Hence, statement-3 is also correct.
th e area under a conditional PDF is always equal to 1. Hence, statement-3 is also correct.