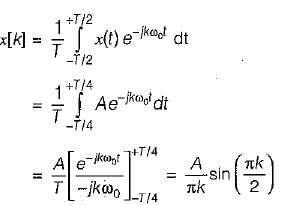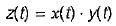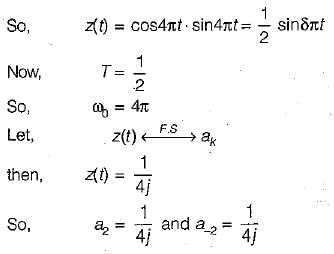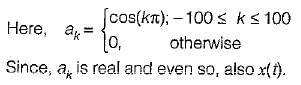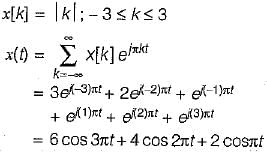Test: Continuous Time Fourier Series - Electronics and Communication Engineering (ECE) MCQ
8 Questions MCQ Test - Test: Continuous Time Fourier Series
If, f(t) = -f(-t)and f(t) satisfy the dirichlet conditions then f(t) can be expanded in a fourier series containing
The trigonometric Fourier series expansion of an odd function shall have
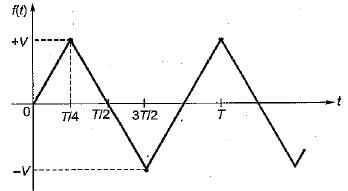
A periodic triangular wave is shown in figure its fourier components will consists only of

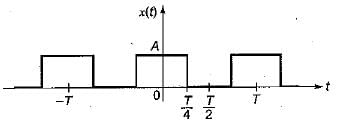
Determine the Fourier series coefficient for given periodic signal x(t) is
Consider the three continuous time signals with fundamental period of T = 1/2
x(t) = cos4πt
y(t) = sin 4πt
z(t) = x(t)·y(t)
The Fourier co-efficient of z(t) are given by
Consider a continuous time periodic signal x(t) given by
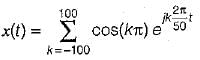
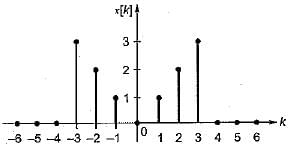
The Fourier series coefficient of time domain signal have been given. Determine the corresponding time domain signal and choose correct option.
The Fourier series for f(x) = sin2 x defined over the range -π ≤ x ≤ π is