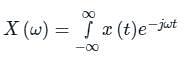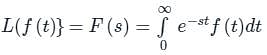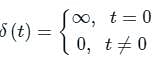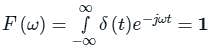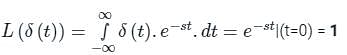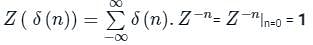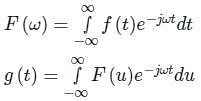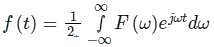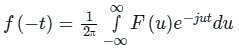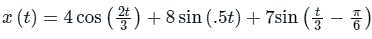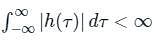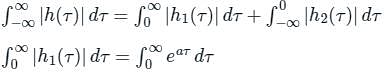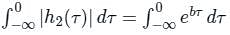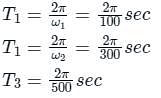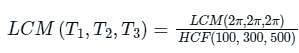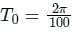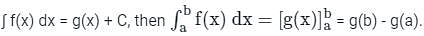Test: Continuous Time Signals - Electrical Engineering (EE) MCQ
10 Questions MCQ Test Signals and Systems - Test: Continuous Time Signals
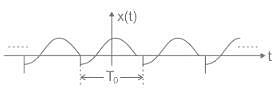
The condition for periodicity of continuous time signal is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
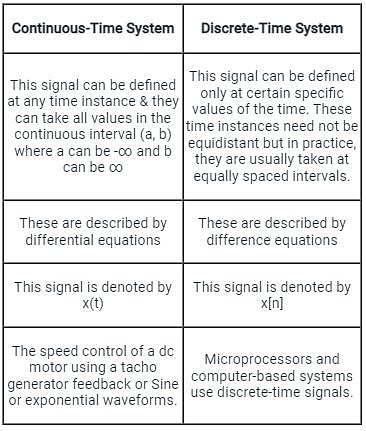
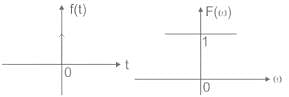
The function which has its Fourier transform, Laplace transform and Z-transform unity is
Let f(t) be a continuous-time signal and let F(ω) be its Fourier Transform defined by

Define g(t) by

What is the relationship between f(t) and g(t)?
Consider a signal x(t) = 4 cos (2t/3) + 8 sin (0.5t) + 7 sin (t/3 – π/6)
Calculate the fundamental period.
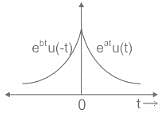
The impulse response h(t) of a continuous time, linear time invariant system is described by h(t) = eat u(t) + ebt u(-t) where, u(t) denots the unit step function and a and b are real constants. This system is stable if
A sinusoidal signal x(t) = 2sin(100t + π/3) is passed through a square law device defined by input-output relation y(t) = x2(t), then the DC component in the signal is:
Consider the following system ‘S’ where x(n) is the input and y(n) is the output

For a periodic signal v(t) = 30 sin100t + 10 cos300t + 6 sin(500t + π/4), the fundamental frequency in rad/s is _____.
A moving average function is given by 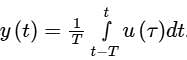 . If the input u is a sinusoidal signal of frequency
. If the input u is a sinusoidal signal of frequency  , then in steady state, the output will lag u (in degree) by
, then in steady state, the output will lag u (in degree) by
|
41 videos|52 docs|33 tests
|
|
41 videos|52 docs|33 tests
|