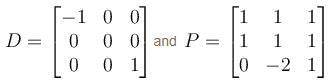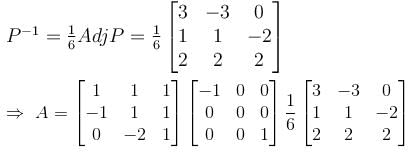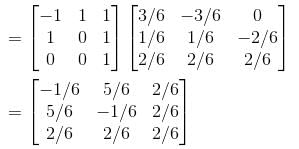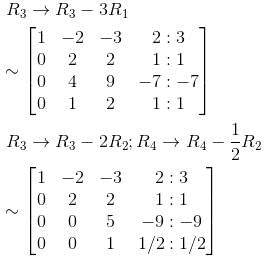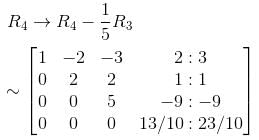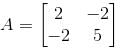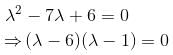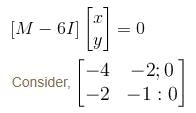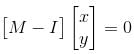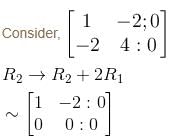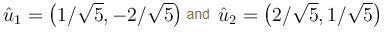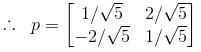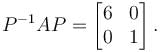Linear Algebra NAT Level - 2 - IIT JAM MCQ
10 Questions MCQ Test - Linear Algebra NAT Level - 2
If (a, 6) are the values for which the given equations are inconsistent.
x + 2y + 3z = 4
x + 3y + 4z = 5
x + 3y + az = b
then the value of a is :
x + 2y + 3z = 4
x + 3y + 4z = 5
x + 3y + az = b
If z = 7c, then find the value of x such that the given equations has infinite solution
x + 3y – 2z = 0
2x – y + 4z = 0
x – 11y + 14z = 0
x + 3y – 2z = 0
2x – y + 4z = 0
x – 11y + 14z = 0
A matrix M has eigenvalues 1 and 4 with corresponding eigenvectors (1, –1)T and (2, 1)T respectively. Then M is given by 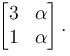 Find the value of α
Find the value of α
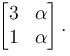 Find the value of α
Find the value of αThe only real value of λ for which the following equations have non-zero solution is,
x + 3y + 3z = λx
3x + y + 2z = λy
2x + 3y + z = λz
For what value of c the following given equations will have infinite number of solutions?
–2x + y + z = 1
x – 2y + z = 1
x + y – 2z = c
Find the rank of the matrix for the following equations :
3x + 4y – z – 6w = 0
2x + 3y + 2z – 3w = 0
2x + y – 14z – 9w = 0
x + 3y + 13z + 3w = 0
Let A be a 3 × 3 matrix. Suppose that the eigenvalues of A are –1, 0, 1 with respective eigenvectors (1,–1,0)T, (1,1,–2)T & (1,1,1)T. Then 6A is given by 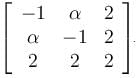 Find the value of α
Find the value of α
Find the rank of the matrix for the following equations :
4x + 2y + z + 3u = 0
6x + 3y + 4z + 7u = 0
2x + y + u = 0
Solution of the system,
3x – 2y – w = 2
2y + 2z + w = 1
x – 2y – 3z + 2w = 3
y + 2z + w = 1
is given by (1, 0, 0, α)T. Find the value of α.
Let  a real symmetric matrix. P is the orthogonal matrix such that P-1 AP is a diagonal matrix given by
a real symmetric matrix. P is the orthogonal matrix such that P-1 AP is a diagonal matrix given by 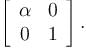 Find the value of α
Find the value of α


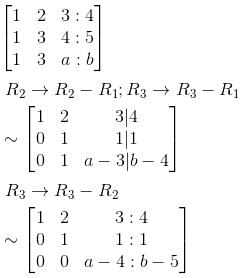
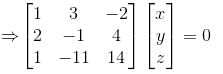
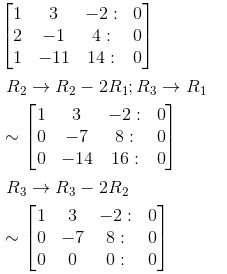
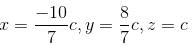

 matrices P and D such that,
matrices P and D such that,
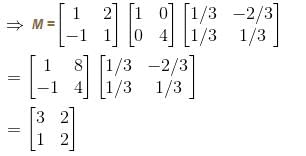
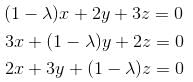
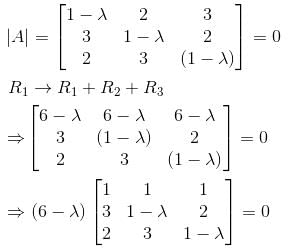
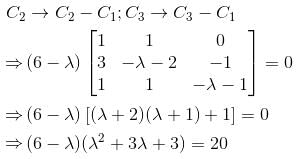
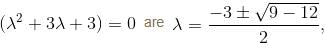 are imaginary.
are imaginary.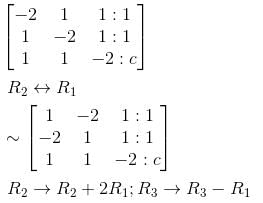
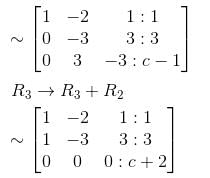

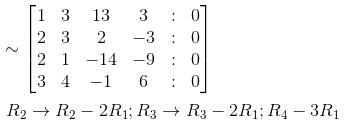
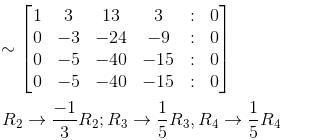
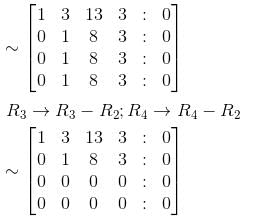
 the matrices D and P such that D = P–1AP is a diagonal matrix.
the matrices D and P such that D = P–1AP is a diagonal matrix.