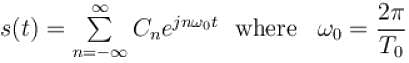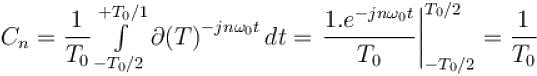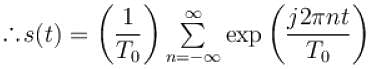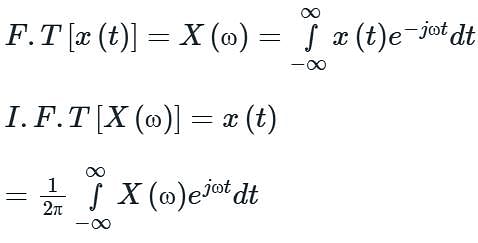Test: Fourier Series- 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test Signals and Systems - Test: Fourier Series- 1
The Fourier series expansion of a real periodic signal with fundamental frequency f0 is given by
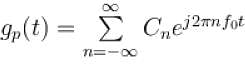
It is given that C3 = 3 + 5j then C-3 is
Select one:
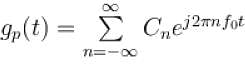
It is given that C3 = 3 + 5j then C-3 is
Select one:
The Fourier series of an odd periodic function, contains only
Select one:
Select one:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following cannot be the Fourier series expansion of a periodic signals?
Select one:
Select one:
A periodic signal x(t) of period T0 is given by

The dc component of x(t) is
Select one:
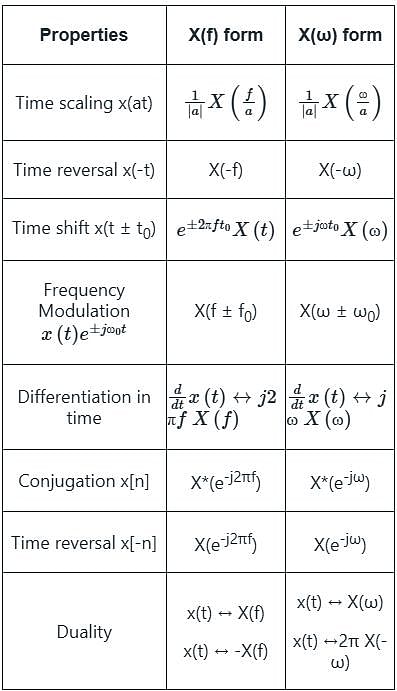
The trigonometric Fourier series of an even function does not have the
Select one:
Choose the function  for which a Fourier series cannot be defined
for which a Fourier series cannot be defined
Select one:
The Fourier series of a real periodic function has only
P. Cosine terms if it is even
Q. Sine terms if it is even
R. Cosine terms if it is odd
S. Sine terms if it is odd
Which of the above statement is correct?
Select one:
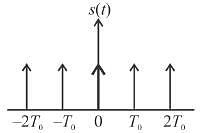
The Fourier series representation of an impulse train denoted by
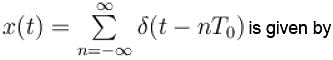
Select one:
Fourier transform of a discrete and aperiodic sequence is:
|
41 videos|52 docs|33 tests
|
|
41 videos|52 docs|33 tests
|



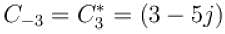
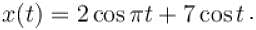 The frequency of first term frequency of 2nd term is ω2 = 1.
The frequency of first term frequency of 2nd term is ω2 = 1.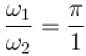 is not the rational number
is not the rational number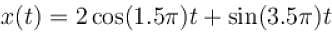 first term has frequency
first term has frequency 
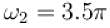

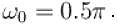

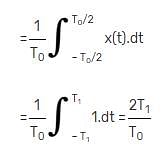
 sin 25t Due to decaying exponential decaying function it is not periodic.
sin 25t Due to decaying exponential decaying function it is not periodic.