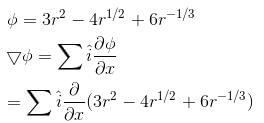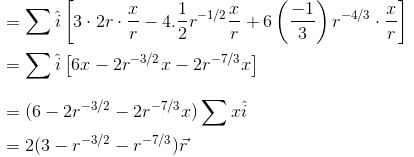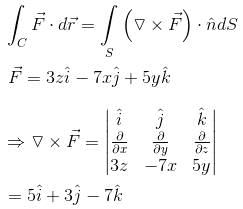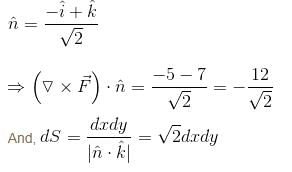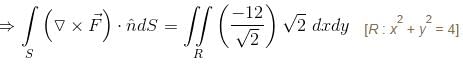Vector Calculus MCQ Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Vector Calculus MCQ Level - 1
The angle between the x2 + y2 + z2 = 9 and z = x2 + y2 – 3 at the point (2, –1, 2) is :
For 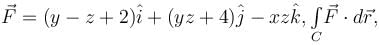 where C is the square in xy–plane projected from the cube x = 0, x = 2, y = 0, y = 2, z = 0, z = 2 above xy–plane, will be equal to :
where C is the square in xy–plane projected from the cube x = 0, x = 2, y = 0, y = 2, z = 0, z = 2 above xy–plane, will be equal to :
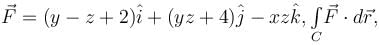 where C is the square in xy–plane projected from the cube x = 0, x = 2, y = 0, y = 2, z = 0, z = 2 above xy–plane, will be equal to :
where C is the square in xy–plane projected from the cube x = 0, x = 2, y = 0, y = 2, z = 0, z = 2 above xy–plane, will be equal to :| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If  and C is the curve y = x3 from the point (1, 1) to (2, 8), then
and C is the curve y = x3 from the point (1, 1) to (2, 8), then 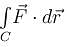 will be :
will be :
 and C is the curve y = x3 from the point (1, 1) to (2, 8), then
and C is the curve y = x3 from the point (1, 1) to (2, 8), then 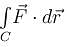 will be :
will be :The value of 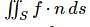 where
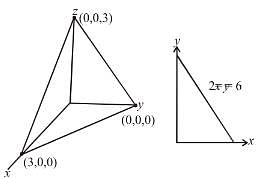
where 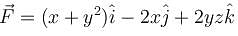 and S in the surface of the plane 2x + y + 2z = 6 in the first octant will be
and S in the surface of the plane 2x + y + 2z = 6 in the first octant will be
A vector field which has a vanishing divergence is called as ____________
The value of the line integral 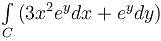 where, C is the boundary of the region lying between the squares with vertices (1, 1), (–1, 1), (–1, –1) and (1, –1) and (2, 2), (–2, 2), (–2, –2) and (2, -2) will be :
where, C is the boundary of the region lying between the squares with vertices (1, 1), (–1, 1), (–1, –1) and (1, –1) and (2, 2), (–2, 2), (–2, –2) and (2, -2) will be :
The value of 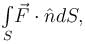 where,
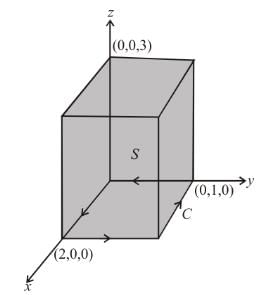
where, 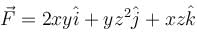 and S is the surface of the parallelepiped bounded by x = 0, y = 0, z = 0, x = 2, y = 1, z = 3 will be :
and S is the surface of the parallelepiped bounded by x = 0, y = 0, z = 0, x = 2, y = 1, z = 3 will be :
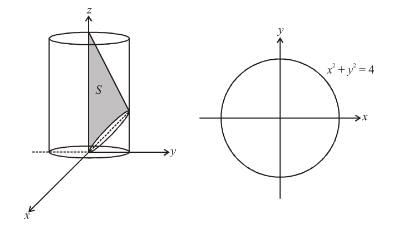
The value of 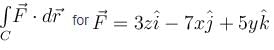 where C is the intersection of z = x + 4 with x2 + y2 = 4 will be :
where C is the intersection of z = x + 4 with x2 + y2 = 4 will be :



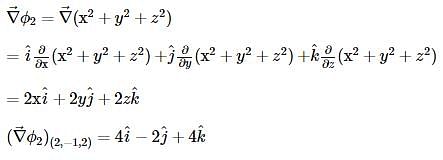
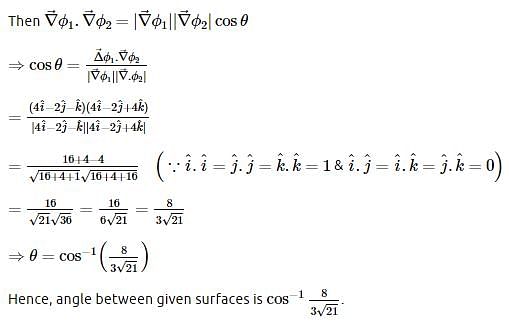



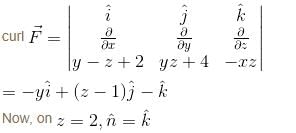
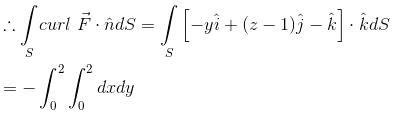
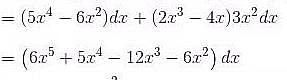
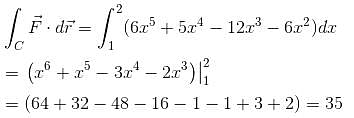
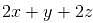 = constant will be :
= constant will be :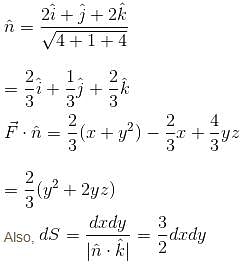
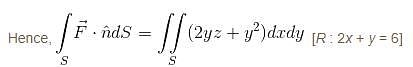
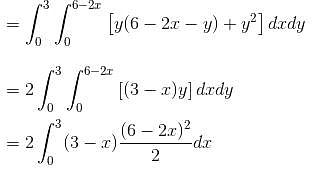
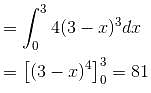


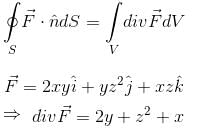
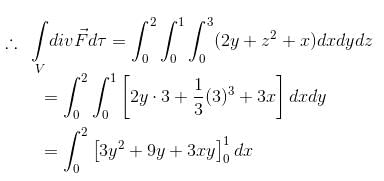
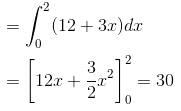
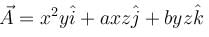 and
and 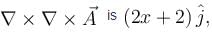 then (a, b) =
then (a, b) =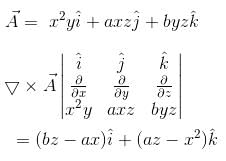
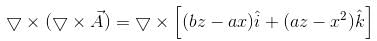

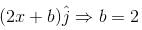
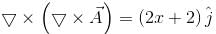
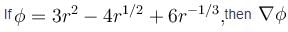 is equal to :
is equal to :