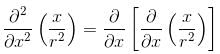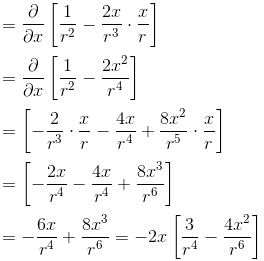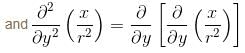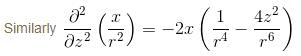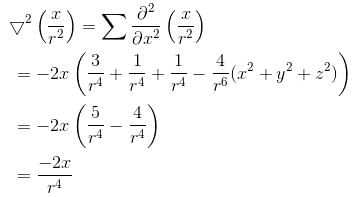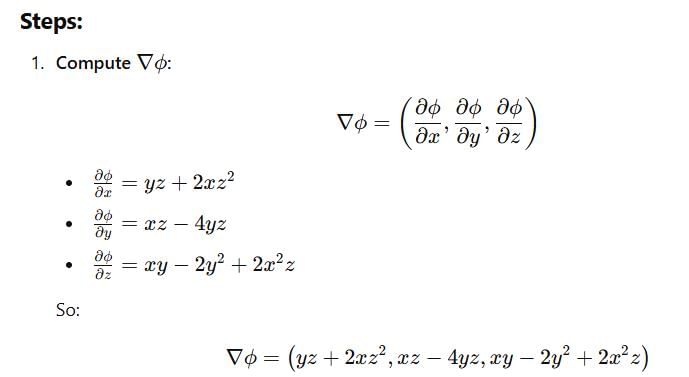Vector Calculus MCQ Level - 2
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics | Vector Calculus MCQ Level - 2
| 1 Crore+ students have signed up on EduRev. Have you? |
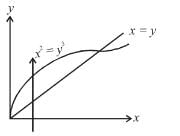
The line integral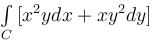 
taken along the closed path formed by y = x and x2 = y3 in the first quadrant will be valuated to :
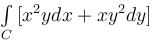taken along the closed path formed by y = x and x2 = y3 in the first quadrant will be valuated to :By Green's theorem, we have,
The correct answer is: 1/198
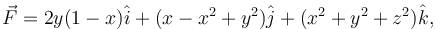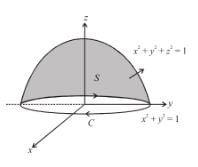
where S : x2 + y2 + z2 = 1, z ≥ 0 and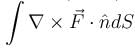 
will have the value :
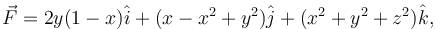where S : x2 + y2 + z2 = 1, z ≥ 0 and 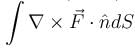will have the value :By Stoke’s Theorem,
where C : x2 + y2 = 1, z = 0
The correct answer is: -π
The line integral of the vector field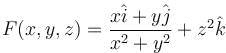 
along the helix defined by x = cos t, y = sin t, 
is equal to :
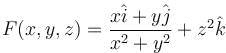along the helix defined by x = cos t, y = sin t, is equal to :We have,
Hence, the line integral of the given vector field will be,
The correct answer is: 1/3
If u = x + y + z, v = x2 + y2 + z2 and w = yz = zx + xy then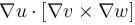 
is equal to :
u = x + y + z
= 0
The correct answer is: 0
The potential function for the vector field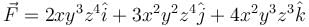 
will be :
Compare the given vector field with the gradient of some function, say φ, i.e.,
⇒ The potential function for the given vector field would be x2y3z4.
The correct answer is: x2y3z4
The value of the surface integral 
where S is the closed surface of the solid bounded by the graphs of x = 4 and z = 9 – y2 and coordinate planes &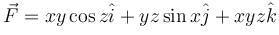 
will be given by :
The given surface is z + y2 = 9
The correct answer is: 
The value of the integral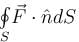 
where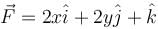 
and where S is the entire surface of the paraboloid z = 1 - x2 - y2 with z = 0 together with the disk {(x, y) : x2 + y2 < 1}
By Gauss Divergence Theorem,
The correct answer is: 2π
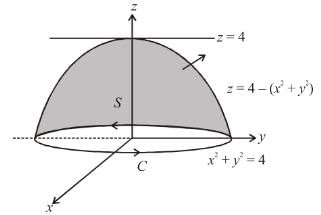
The value of 
where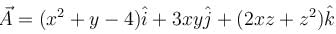 
and S is the surface of the paraboloid z = 4 – (x2 + y2) above the xy-plane will be :
By Stokes theorem,
Here, the boundary curve C of the surface will be given by x2 + y2 = 4, z = 0, or 
The correct answer is: -4π
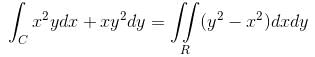
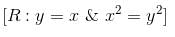
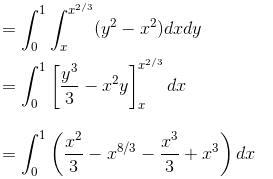
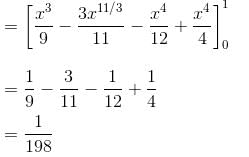
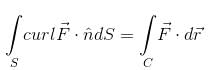
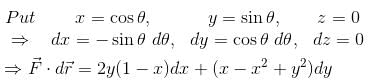
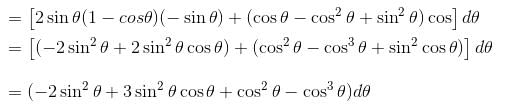
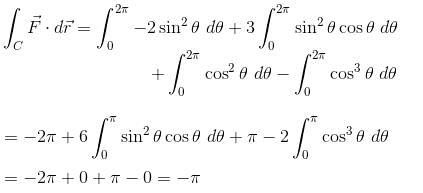
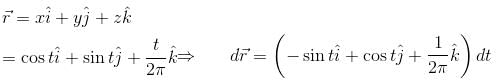
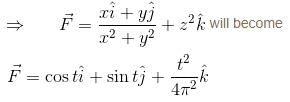
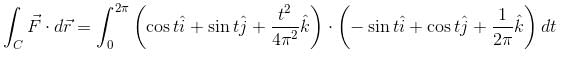
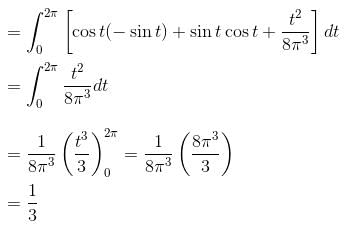
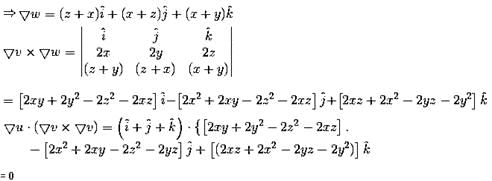
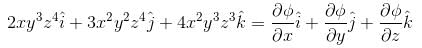
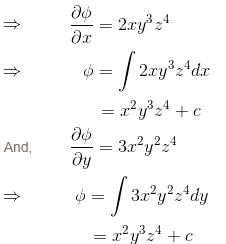
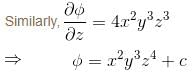
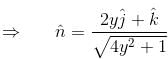
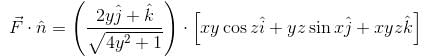
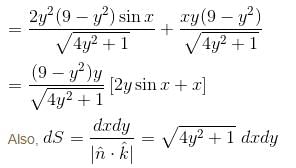
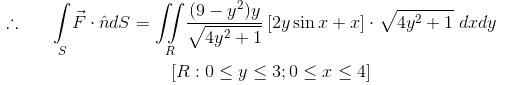
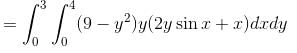
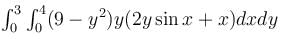
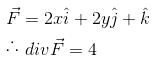
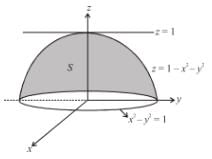
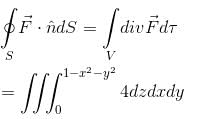
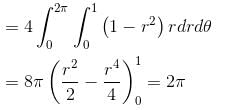
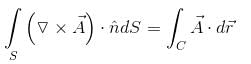
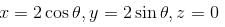
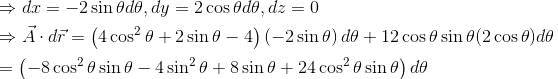
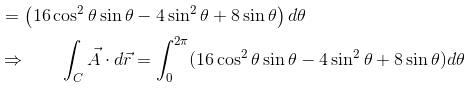
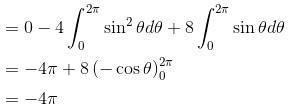
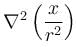is equal to :Consider, 
The correct answer is: 
is equivalent to :
The correct answer is: 
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Download free EduRev App
Related content with Vector Calculus MCQ Level - 2
|
|
|
Related tests with Vector Calculus MCQ Level - 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
