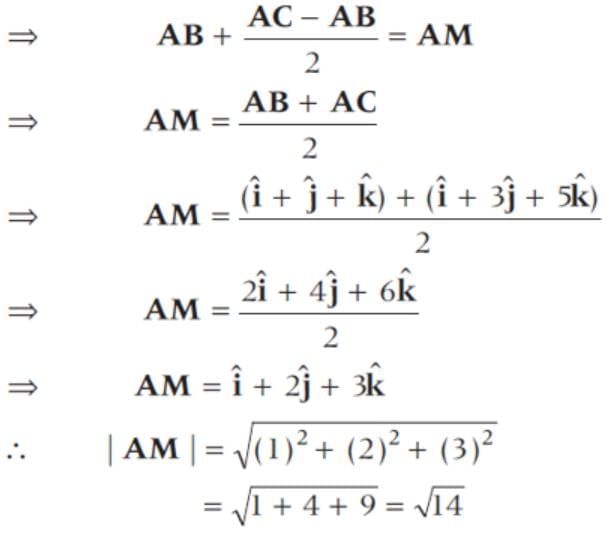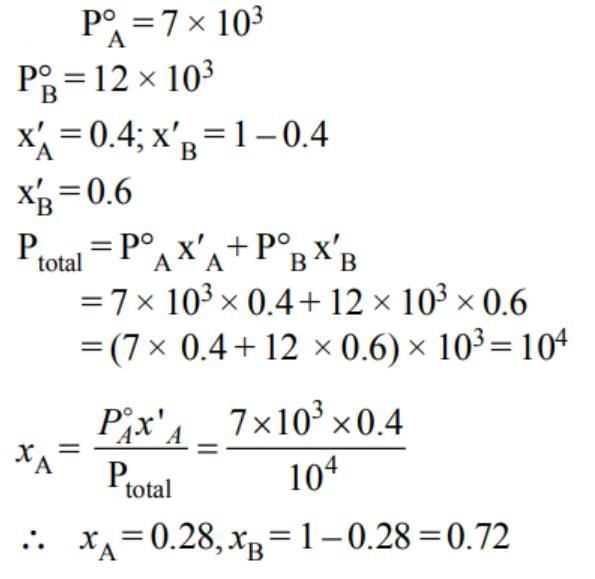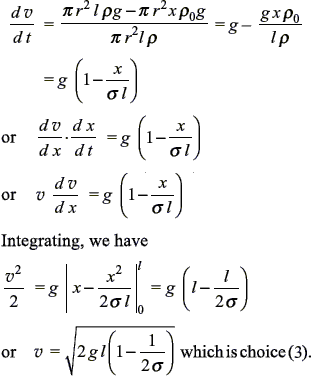UGEE SUPR Mock Test-1 - JEE MCQ
30 Questions MCQ Test - UGEE SUPR Mock Test-1
A vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
A body of density ρ is dropped from rest from a height h into a lake of density σ, where σ > ρ. Neglecting all dissipative forces, the maximum depth to which the body sinks before returning to float on surface
The heat generated in a circuit is given by Q = I2 Rt, where I is current, R is resistance andt is time. If the percentage errors in measuring I, R and t are 2%, 1% and 1% respectively, thenthe maximum error in measuring heat will be
The r.m.s. velocity of oxygen molecule at 16°C is 474 m/sec. The r.m.s. velocity in m/s of hydrogen molecule at 127°C is
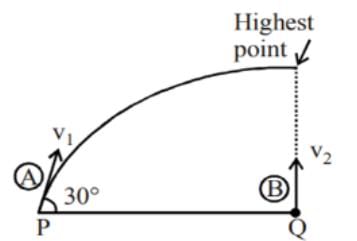
A projectile A is thrown at an angle of 30° to the horizontal from point P. At the same time, another projectile B is thrown with velocity v2 upwards from the point Q vertically below the highest point. For B to collide with A, v2/v1 should be
The coefficient of friction between the rubber tyres and the road way is 025. The maximum speed with which a car can be driven round a curve of radius 20 m without skidding is (g = 9.8 m/s2)
A boy pushes a toy box 2.0 m along the floor by means of a force of 10 N directed downward at an angle of 60° to the horizontal. The work done by the boy is
The engine of a truck moving along a straight road delivers constant power. The distance travelled by the truck in time t is proportional to
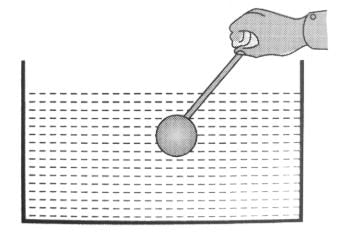
A vessel with water is placed on a weighing pan and reads 600g. Now a ball of 40g and density 0.80g/cc is sunk into the water with a pin as shown in fig. keeping it sunk. The weighing pan will show a reading
In an adiabatic process, the pressure is increased by 2/3%. If γ = 3/2 then the volume decreases by nearly
The length of the latus rectum of the parabola which has focus at (-1, 1) and the directrix is given by the line equation 4x+2y - 3=0
A student read the common difference of an A.P. as -2 instead of 2 and got the sum of the first 5 terms as -5. Actual sum of first five terms is
If 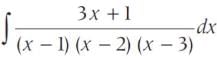 = A log |x − 1| + B log |x − 2| + C log |x − 3| + C, then the values of A, B, C are respectively
= A log |x − 1| + B log |x − 2| + C log |x − 3| + C, then the values of A, B, C are respectively
The area of the region bounded by the curve y2 = 8x and the line y = 2x is
The order of the differential equation obtained by eliminating arbitrary constants in the family of curves c1y = (c2 + c3)ex +c4 is
The general solution of the differential equation x2dy - 2xydx = x4 cos xdx is
The area of the region bounded by the line y = 2x + 1, X-axis and the ordinates x = -1 and x = 1 is
The two vector 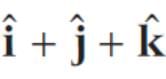 and
and 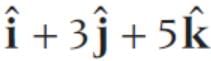 represent the two sides
represent the two sides 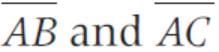 respectively of a ΔABC. The length of the median through A is
respectively of a ΔABC. The length of the median through A is
If A is a square matrix of order 3 and |A| = 5, then |A adj. A| is
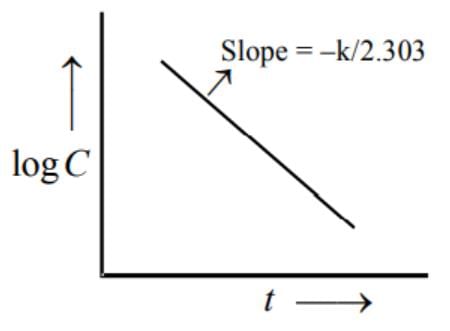
In a 1st order reaction, reactant concentration C varies with time t as:
Which of the following set contains species having same angle around the central atom?
Note: Ignore Lone pair bond pair repulsion
Liquids A and B form an ideal solution in the entire composition range. At 350 K, the vapor pressures of pure A and pure B are 7 × 103 Pa and 12 × 103 Pa, respectively. The composition of the vapour is in equilibrium with a solution containing 40 mole percent of A at this temperature is:
Hydrolysis of NCl3 gives NH3 and X. Which ofthe following is X ?
Element 'B' forms ccp structure and 'A' occupies half of the octahedral voids, while oxygen atoms occupy all the tetrahedral voids. The structure of bimetallic oxide is :
A long metal rod of length l and relative density σ is held vertically with its lower end just touching the surface of water. The speed of the rod, when it just sinks in water, is given by


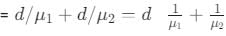 , which matches option B.
, which matches option B.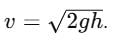
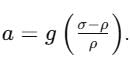
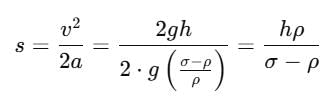

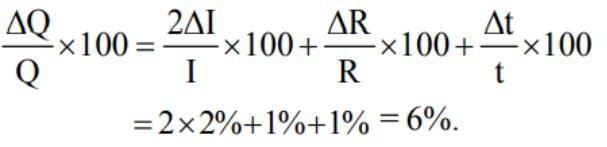
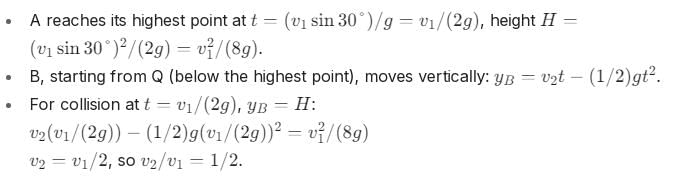
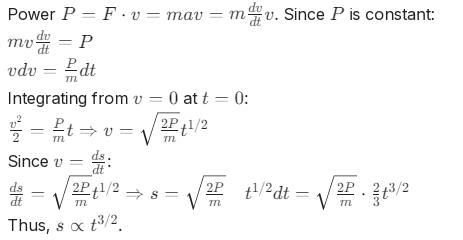




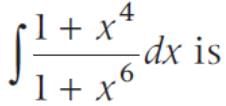
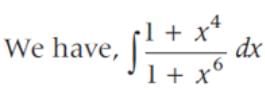
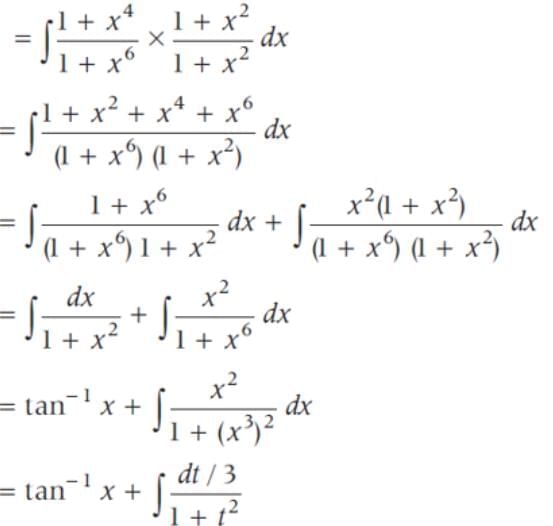
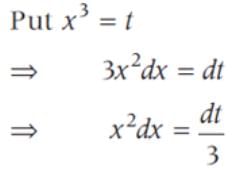
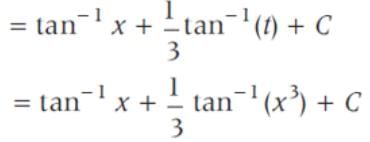
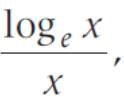 if x > 0 is
if x > 0 is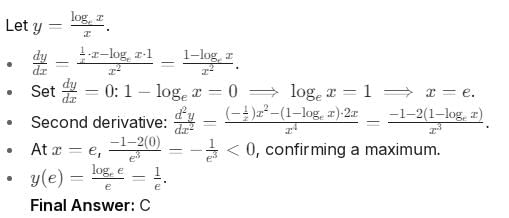
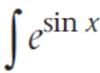 sin2 x dx is
sin2 x dx is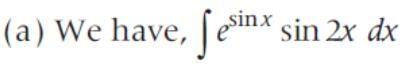
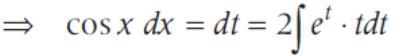
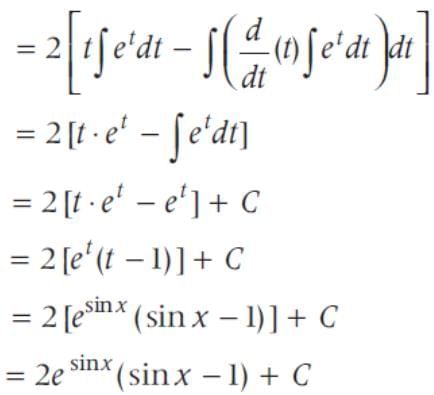
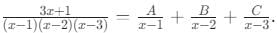



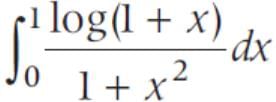 is
is

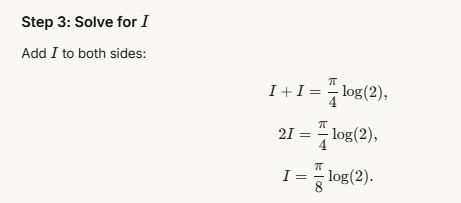
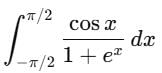 is
is 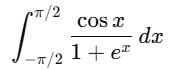
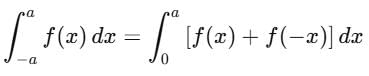
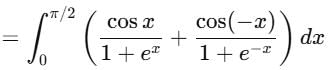
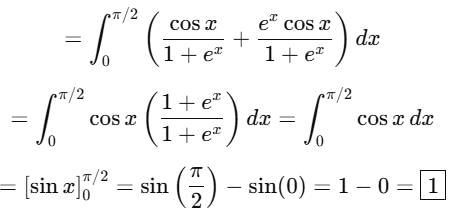
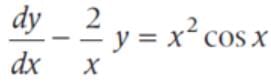
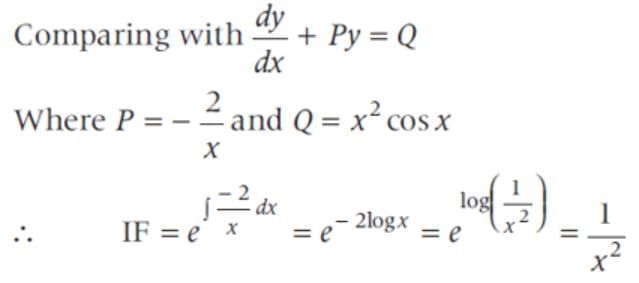
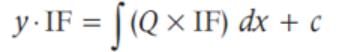
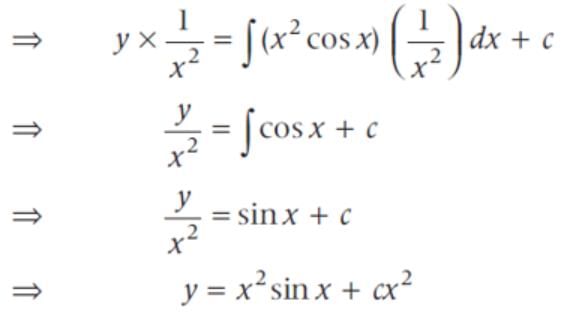
 and (0, 1).
and (0, 1).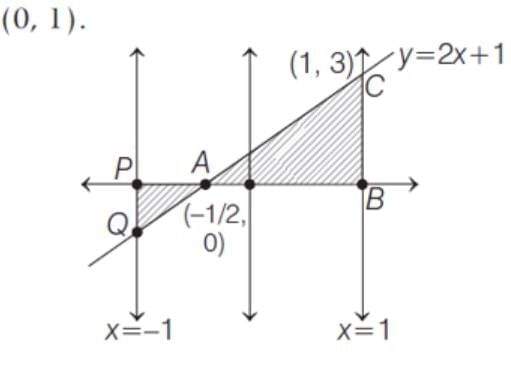


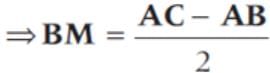 (since, M is a mid-point of BC)
(since, M is a mid-point of BC)