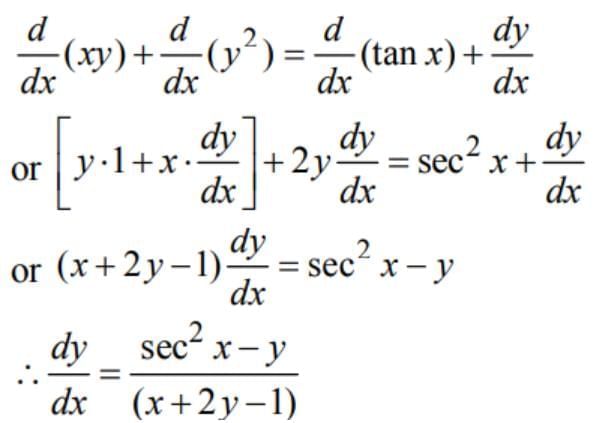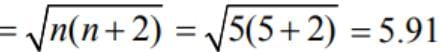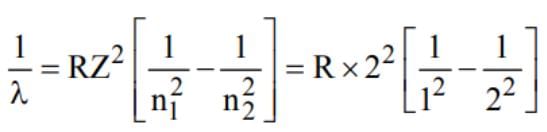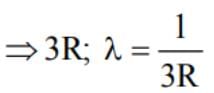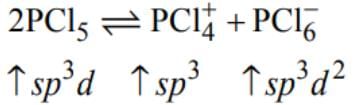UGEE SUPR Mock Test-2 - JEE MCQ
30 Questions MCQ Test - UGEE SUPR Mock Test-2
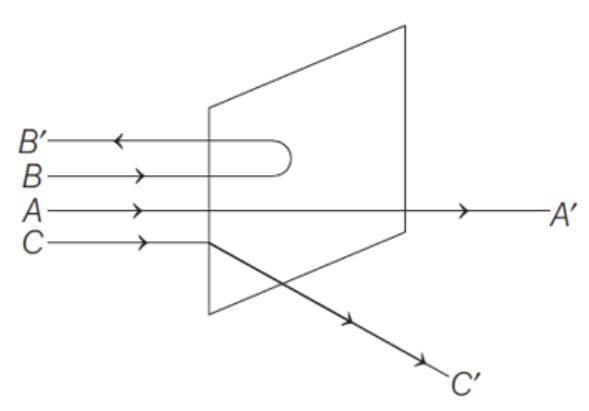
A beam of fast moving alpha particles were directed towards a thin film of gold. The parts A, B and C of the transmitted and reflected beams corresponding to the incident parts A, B and C of the beam are shown in the adjoining diagram. The number of alpha particles in

A radio-active elements has half-life of 15 years. What is the fraction that will decayin 30 years?
Two long straight parallel wires are a distance d part. They carry steady equal currents flowing out of the plane of the paper. The variation of magnetic field B along the line xx' is given by
A cylindrical wire has a mass (0.3 ± 0.003)g, radius (0.5±0.005) mm and length (6 ± 0.06)cm. The maximum percentage error in the measurement of its density is
At a metro station, a girl walks up a stationary escalator in 20s. If she remains stationary on the escalator, then the escalator take her upin 30 s. The time taken by her to walk up on the moving escalator will be
Rain is falling vertically with a speed of 12 ms-1. A woman rides a bicycles with aspeed of 12 ms-1 in east to west direction.What is the direction in which she shouldhold her umbrella?
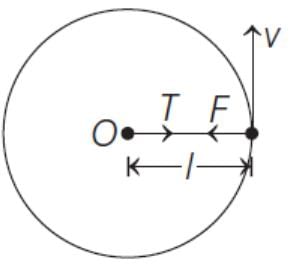
One end of a string of length I is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v, the net force on the particle (directed towards the centre) is (T is the tension in the string)
A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
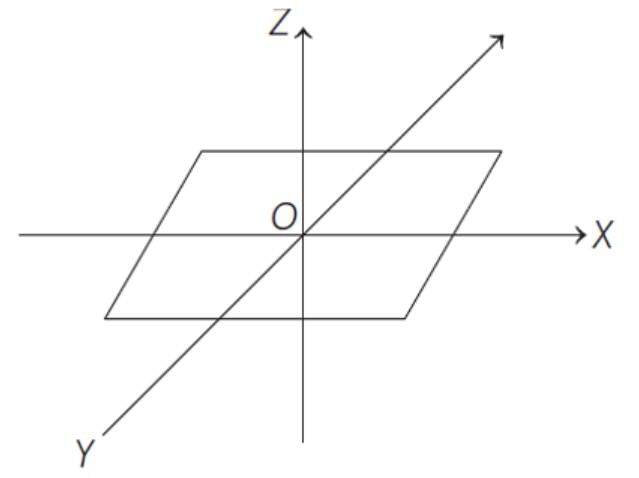
A thin uniform rectangular plate of mass 2 kg is placed in xy-plane as shown in figure.
The moment of inertial about x-axis is Ix = 0.2 kgm2 and the moment of inertia about Y-axis is ly = 0.3 kgm2. The radius of gyration of the plate about the axis passing through O and perpendicular to the plane of the plate is
The right hand and left hand limit of the function are respectively.
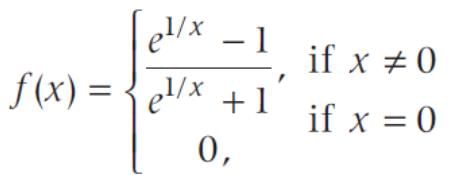
If 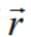 and
and 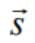 are non-zero constant vectors and the scalar b is chosen such that
are non-zero constant vectors and the scalar b is chosen such that 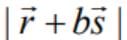 is minimum, then the value of
is minimum, then the value of 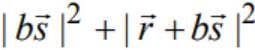 is equal to
is equal to
Statement-I : If the general equation x2 + y2 + 2xy + 2gx + 2fy + 4 = 0 represents a pair of real lines then |g| ≥ 2.
Statement-2 : The equation ax2 + 2hxy + by2 + 2gx + 2fy+ c = 0 represents pair of real lines if abc + 2fgh - af2 - bg2 - ch2 = 0.
The number of possible outcomes in a throw of n ordinary dice in which at least one of the dice shows an odd number is
Which one of the following ions has the maximum magnetic moment?
For which one of the processes represented by the following equations the enthalpy (heat) change is likely to be negative
Phosphine is not obtained by which of thefollowing reaction ?
What is the maximum wavelength line in the Lyman series of He+ ion?
In the reaction 2 PCl5 ⇌ + PCI+4 + PCl-6 , the change in hybridisation is from
Arrange the following ions in the order decreasing X — O bond length, where X is the central atom
Two vessels of volumes 16.4 L and 5 L contain two ideal gases of molecular existence at the respective temperature of 27°C and 227°C and exert 1.5 and 4.1 atmospheres respectively. The ratio ofthe number of molecules of the former to that of the later is
For the combustion reaction at 298 K
2Ag(s) + 1 / 2O2 (g) → 2Ag2O(s)
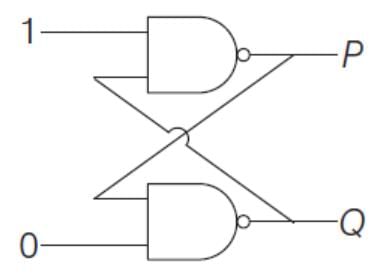
Which ofthe following alternatives is correct?
Note: Count Solid State also in this question.


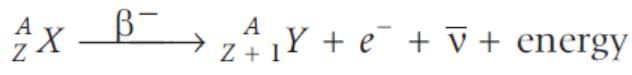

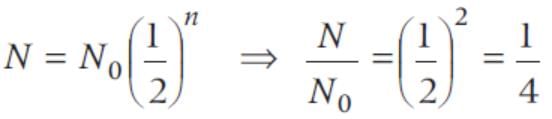
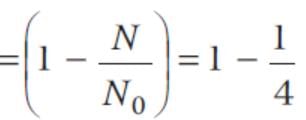
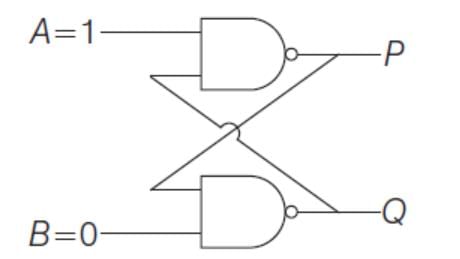

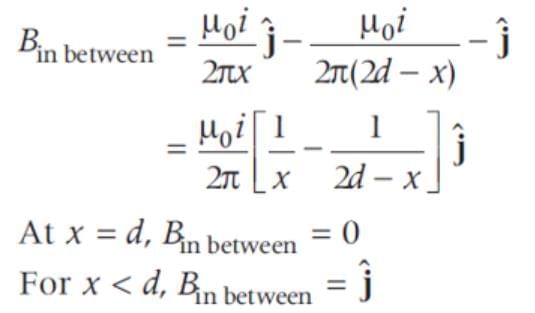
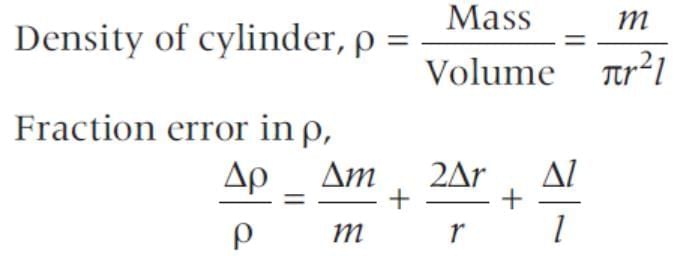
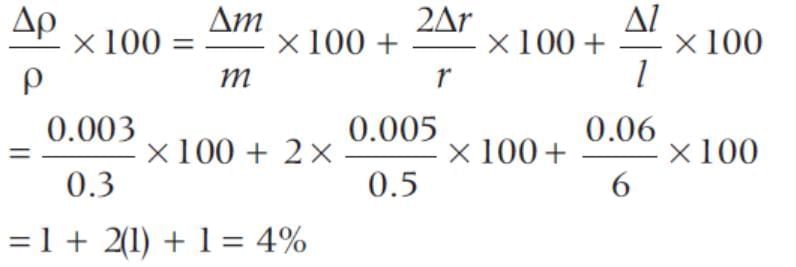
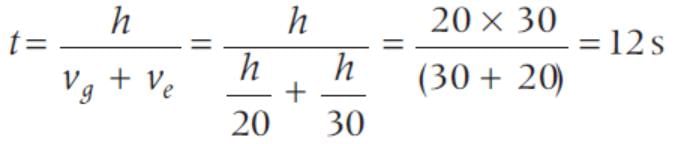
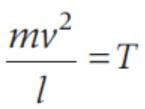
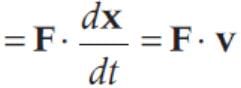
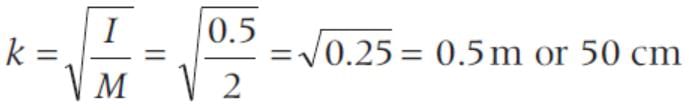



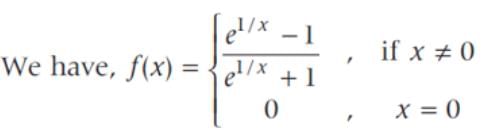
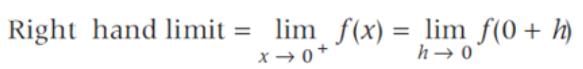
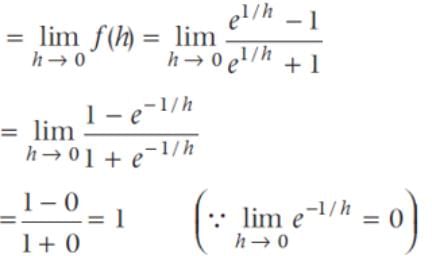
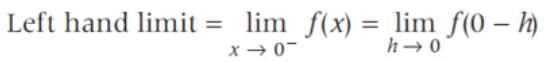
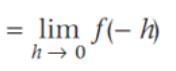
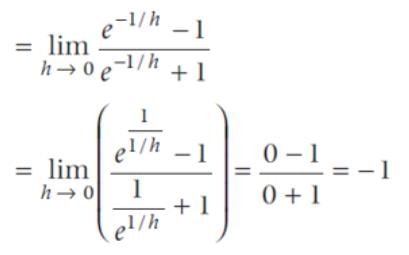
 is
is
 = 0.
= 0. and
and 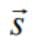 are anti-parallel so
are anti-parallel so 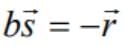
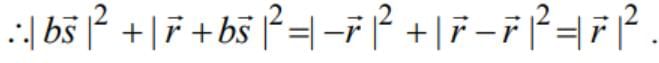
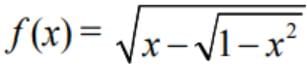 is
is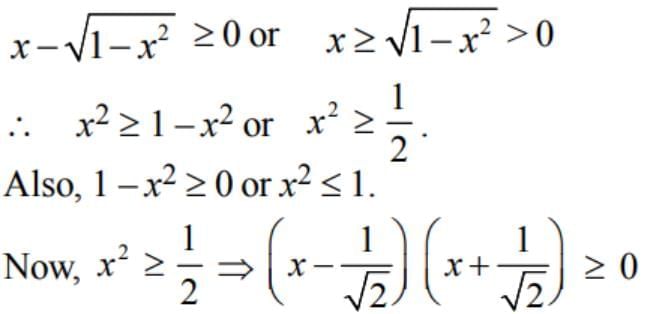
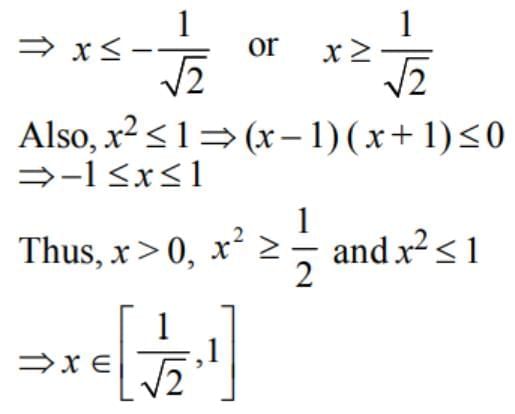
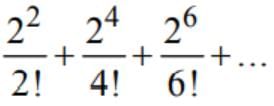 is equal to
is equal to