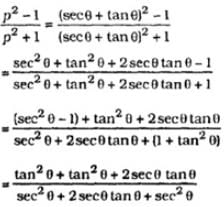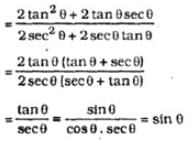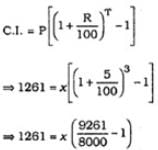RRB JE ECE (CBT I) Mock Test- 3 - Electronics and Communication Engineering (ECE) MCQ
30 Questions MCQ Test RRB JE Mock Test Series for ECE 2025 - RRB JE ECE (CBT I) Mock Test- 3
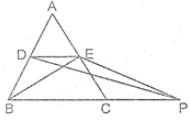
D and E are the mid-points of AB and AC of ∆ABC, BC is produced to any point P; DE, DP and EP are joined. then, area of:
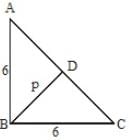
One side other than the hypotenuse of the right angle isosceles triangle is 6 cm. The length of the perpendicular on the hypotenuse from the opposite vertex is:
The speeds of two trains are in the ratio 3: 4. They are going in opposite directions along parallel tracks. If each takes 3 seconds to cross a telegraph post, find the time taken by the trains to cross each other completely?
A mother is 3 times faster than her daughter. If the daughter completes a piece of work in 15 days, how long will it take for both mother and daughter to complete the same work?
Study the following table carefully to answer the questions that follow.
The number of soldiers (in thousands) joining five different forces during six different years.
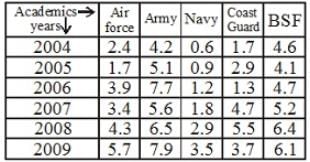
The total number of soldiers joining BSF in the years 2004, 2005 and 2006 was approximately what percent of the total number of soldiers joining the Navy over all the years together?
Study the following table carefully to answer the questions that follow.
The number of soldiers (in thousands) joining five different forces during six different years.
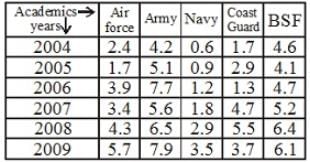
What was the ratio of the number of soldiers joining the Army in the year 2008 to the number of soldiers joining the coast guard in the year 2006?
If tan (5x – 10°) = cot (5y + 20°), then the value of (x+y) is:
If a train, with a speed of 60 km/hr, crossed a pole in 30 seconds, the length of the train (in meters) is:
The supplement of an angle is one-fourth of itself. Determine the angle and its supplement.
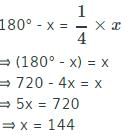
3 years ago the average age of a family of 5 members was 17 years. A baby having been born, the average age of the family is the same today. The present age of the baby is
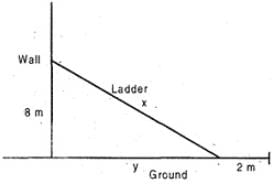
A ladder leans against a vertical wall. The top of the ladder is 8 metres above the ground. When the bottom of the ladder is moved 2 metres farther away from the wall, the top of the ladder rests against the foot of the wall. What is the length of the ladder?
The length of a Rectangular plot is decreased by 33.33%. By how much % the breadth of the plot will be increased so that the area remains constant?
A man deposited a certain amount in a fixed deposit at r % p.α., interest being compounded annually. If the interest accrued for the fourth and fifth years are Rs 13310 and Rs 14641. what is the total interest accrued for the first three years?
A person earns Rs. 5000 as an interest in 5/2 years on a certain sum invested with a company at the rate of 10% per annum. Find the sum invested by a person in the company?
A is twice as fast as B and B is one third as fast as C. If they together can complete work in 30 days. In how many days, A, B and C individually can do the same work?
The price of a shirt is ₹260 but the shopkeeper successively discounts 15% & 20%. The net sales price is subject to a sales tax of 5%. What does the buyer pay?
A cistern from inside is 12.5 m long, 8.5 m broad and 4 m high and is open at the top. Find the cost of cementing the inside of a cistern at Rs. 24 per sq. m
A goat is tied to a pole fixed at a corner outside a room with a square base in a grass field. It is tied using a 14 m long rope. The side of the base of the room is 21 m. Find the area of the field over which the goat can graze (in sq. m).
An article is sold at a loss of 10%. Had it been sold for Rs. 9 more, there would have been a gain of ![]() % on it. The cost price of the article is :
% on it. The cost price of the article is :
A water tank is 6 m long, 5 m broad and 3.4 m high. Find the capacity of the tank in litres?
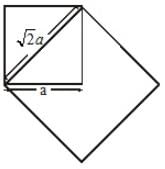
The ratio of the area of a square to that of the square drawn on its diagonal is :
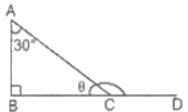
In the given figure, if ∠ABC = 90° and ∠A = 30°, then ∠ACD=
A certain sum of money yields ₹ 1261 as compound interest for 3 years at 5% per annum. The sum is
A is twice as good a workman as B. Together, they finish the work in 14 days. In how many days can it be done by each separately?


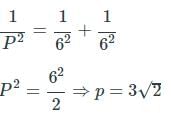

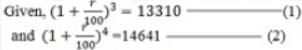
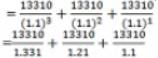
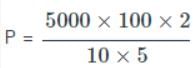
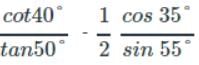 is
is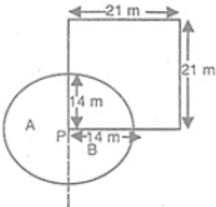
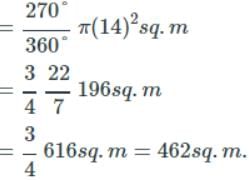
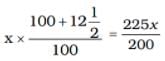
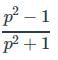 = ?
= ?