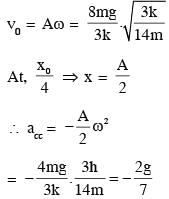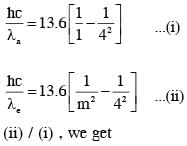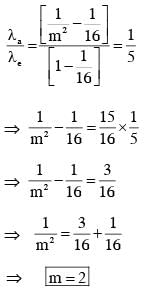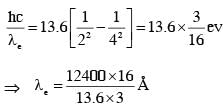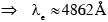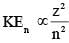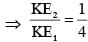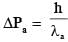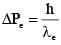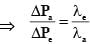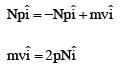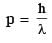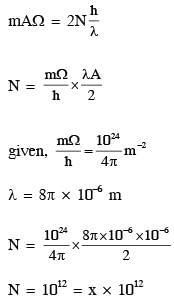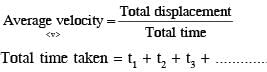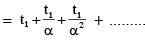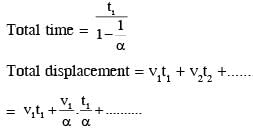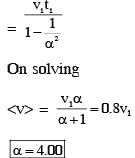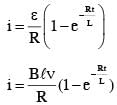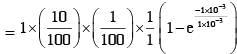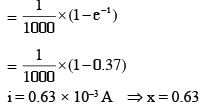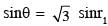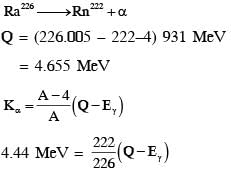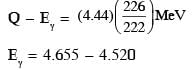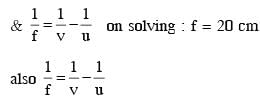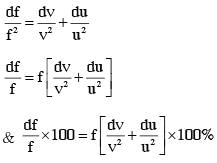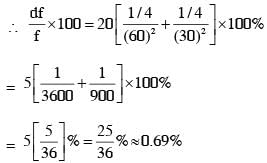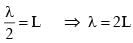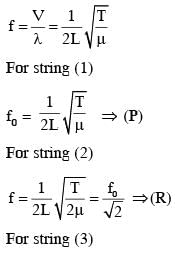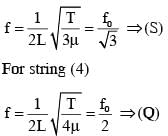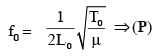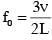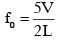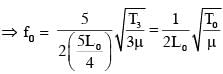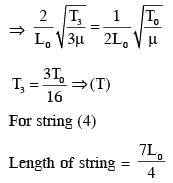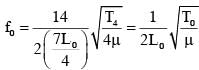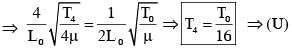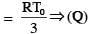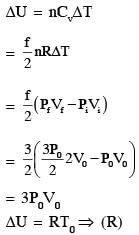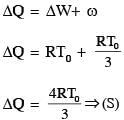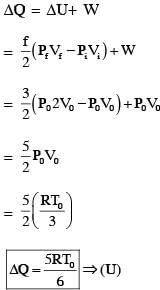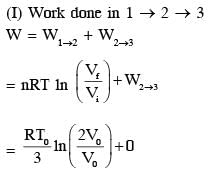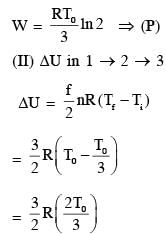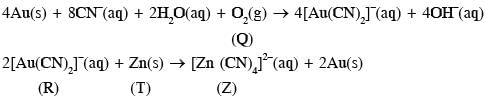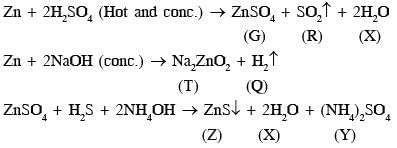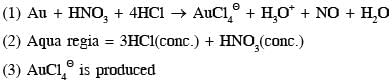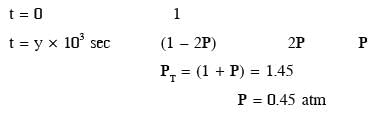JEE Advanced 2019 Question Paper with Solutions (27th May - Evening) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Advanced 2019 Question Paper with Solutions (27th May - Evening)
A mixture of ideal gas containing 5 moles of monatomic gas and 1 mole of rigid diatomic gas is initially at pressure P0, volume V0 and temperature T0. If the gas mixture is adiabatically compressed to a volume V0/4, then the correct statement(s) is/are,
(Give 21.2 = 2.3 ; 23.2 = 9.2; R is gas constant)
(Give 21.2 = 2.3 ; 23.2 = 9.2; R is gas constant)
An electric dipole with dipole moment  is held fixed at the origin O in the presence of an uniform electric field of magnitude E0. If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are:
is held fixed at the origin O in the presence of an uniform electric field of magnitude E0. If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are:
(ε0 is permittivity of free space, R >> dipole size)
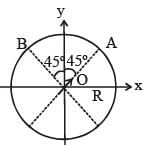
 is held fixed at the origin O in the presence of an uniform electric field of magnitude E0. If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are:
is held fixed at the origin O in the presence of an uniform electric field of magnitude E0. If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are:(ε0 is permittivity of free space, R >> dipole size)

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
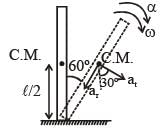
A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping.
Which of the following statement(s) is/are correct, when the rod makes an angle 60º with vertical? [g is the acceleration due to gravity]
Which of the following statement(s) is/are correct, when the rod makes an angle 60º with vertical? [g is the acceleration due to gravity]
A small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from closed end is L = L0 the particle speed is v = v0. The piston is moved inward at a very low speed V such that 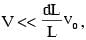 where dL is the infinitesimal displacement of the piston. Which of the following statement(s) is/are correct?
where dL is the infinitesimal displacement of the piston. Which of the following statement(s) is/are correct?
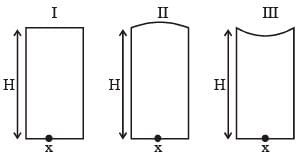
Three glass cylinders of equal height H = 30 cm and same refractive index n = 1.5 are placed on a horizontal surface shown in figure. Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (R = 3m). If H1, H2 and H3 are the apparent depths of a point X on the bottom of the three cylinders, respectively, the correct statement(s) is/are
In a Young's double slit experiment, the slit separation d is 0.3 mm and the screen distance D is 1m. A parallel beam of light of wavelength 600nm is incident on the slits at angle α as shown in figure. On the screen, the point O is equidistant from the slits and distance PO is 11.0 mm. Which of the following statement(s) is/are correct?

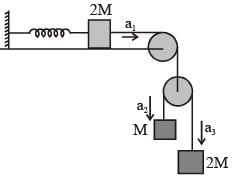
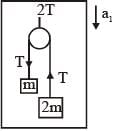
A block of mass 2M is attached to a massless spring with spring constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1, a2 and a3 as shown in figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0. Which of the following option(s) is/are correct? [g is the acceleration due to gravity. Neglect friction]
A free hydrogen atom after absorbing a photon of wavelength λa gets excited from the state n = 1 to the state n = 4. Immediately after that the electron jumps to n = m state by emitting a photon of wavelength λe. Let the change in momentum of atom due to the absorption and the emission are Δpa and Δpe, respectively. If 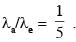 Which of the option(s) is/are correct?
Which of the option(s) is/are correct?
[Use hc = 1242 eV nm; 1 nm = 10–9 m, h and c are Planck's constant and speed of light, respectively]
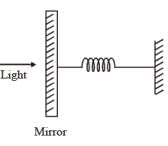
A perfectly reflecting mirror of mass M mounted on a spring constitutes a spring-mass system of angular frequency Ω such that 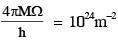 with h as Planck's constant. N photons of wavelength λ = 8π × 10–6m strike the mirror simultaneously at normal incidence such that the mirror gets displaced by 1µm. If the value of N is x × 1012, then the value of x is ____.
with h as Planck's constant. N photons of wavelength λ = 8π × 10–6m strike the mirror simultaneously at normal incidence such that the mirror gets displaced by 1µm. If the value of N is x × 1012, then the value of x is ____.
[Consider the spring as massless]
A ball is thrown from ground at an angle θ with horizontal and with an initial speed u0. For the resulting projectile motion, the magnitude of average velocity of the ball up to the point when it hits the ground for the first time is V1. After hitting the ground, ball rebounds at the same angle θ but with a reduced speed of u0/α. Its motion continues for a long time as shown in figure. If the magnitude of average velocity of the ball for entire duration of motion is 0.8 V1, the value of α is______

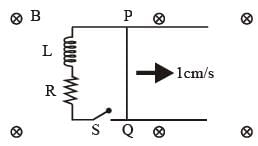
A 10 cm long perfectly conducting wire PQ is moving, with a velocity 1cm/s on a pair of horizontal rails of zero resistance. One side of the rails is connected to an inductor L = 1 mH and a resistance R = 1Ω as shown in figure. The horizontal rails, L and R lie in the same plane with a uniform magnetic field B = 1 T perpendicular to the plane. If the key S is closed at certain instant, the current in the circuit after 1 millisecond is x × 10–3A, where the value of x is_______.
[Assume the velocity of wire PQ remains constant (1 cm/s) after key S is closed. Given: e–1 = 0.37, where e is base of the natural logarithm]
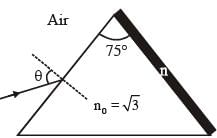
A monochromatic light is incident from air on a refracting surface of a prism of angle 75° and refractive index n0 =√3 . The other refracting surface of a prism is coated by a thin film of material of refractive index n as shown in figure. The light suffers total internal reflection at the coated prism surface for an incidence angle of θ ≤ 60°. The value of n2 is_______.
Suppose a 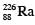 nucleus at rest and in ground state undergoes α-decay to a
nucleus at rest and in ground state undergoes α-decay to a 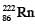 nucleus in its excited state. The kinetic energy of the emitted α particle is found to be 4.44 MeV.
nucleus in its excited state. The kinetic energy of the emitted α particle is found to be 4.44 MeV. 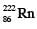 nucleus then goes to its ground state by γ-decay. The energy of the emitted γ-photon is _______ keV,
nucleus then goes to its ground state by γ-decay. The energy of the emitted γ-photon is _______ keV,
[Given: atomic mass of 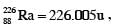 atomic mass of
atomic mass of 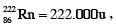 atomic mass of α particle = 4.000u, 1u = 931 MeV/c2, c is speed of the light]
atomic mass of α particle = 4.000u, 1u = 931 MeV/c2, c is speed of the light]
An optical bench has 1.5 m long scale having four equal divisions in each cm. While measuring the focal length of a convex lens, the lens is kept at 75 cm mark of the scale and the object pin is kept at 45 cm mark. The image of the object pin on the other side of the lens overlaps with image pin that is kept at 135 cm mark. In this experiment, the percentage error in the measurement of the focal length of the lens is________.
Answer the following by appropriately matching the lists based on the information given in the paragraph.
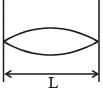
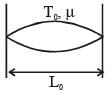
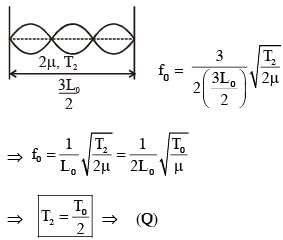
A musical instrument is made using four different metal strings, 1,2,3 and 4 with mass per unit length µ, 2µ, 3µ and 4µ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1 (µ) at free length L0 and tension T0 the fundamental mode frequency is f0.
List-I gives the above four strings while List-II lists the magnitude of some quantity.

If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be,
Answer the following by appropriately matching the lists based on the information given in the paragraph.
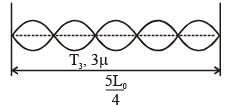
A musical instrument is made using four different metal strings, 1,2,3 and 4 with mass per unit length µ, 2µ, 3µ and 4µ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1 (µ) at free length L0 and tension T0 the fundamental mode frequency is f0.
List-I gives the above four strings while List-II lists the magnitude of some quantity.

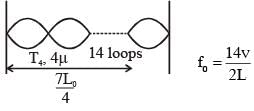
The length of the string 1,2,3 and 4 are kept fixed at 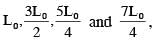 respectively. Strings 1,2,3 and 4 are vibrated at their 1st, 3rd, 5th and 14th harmonics, respectively such that all the strings have same frequency. The correct match for the tension in the four strings in the units of T0 will be.
respectively. Strings 1,2,3 and 4 are vibrated at their 1st, 3rd, 5th and 14th harmonics, respectively such that all the strings have same frequency. The correct match for the tension in the four strings in the units of T0 will be.
Answer the following by appropriately matching the lists based on the information given in the paragraph.
In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by TΔX, where T is temperature of the system and ΔX is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas 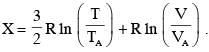 Here, R is gas constant, V is volume of gas, TA and VA are constants.
Here, R is gas constant, V is volume of gas, TA and VA are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

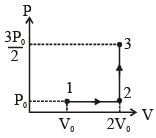
If the process carried out on one mole of monatomic ideal gas is as shown in figure in the PV-diagram with 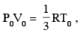 the correct match is,
the correct match is,
Answer the following by appropriately matching the lists based on the information given in the paragraph.
In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by TΔX, where T is temperature of the system and ΔX is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas 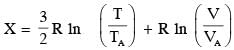 . Here, R is gas constant, V is volume of gas, TA and VA are constants.
. Here, R is gas constant, V is volume of gas, TA and VA are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

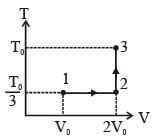
If the process on one mole of monatomic ideal gas is an shown is as shown in the TV-diagram with P0V0 = 1/3 RT0, the correct match is
The cyanide process of gold extraction involves leaching out gold from its ore with CN– in the presence of Q in water to form R. Subsequently, R is treated with T to obtain Au and Z. Choose the correct option(s).
Which of the following reactions produce(s) propane as a major product?
The ground state energy of hydrogen atom is –13.6 eV. Consider an electronic state ψ of He+ whose energy, azimuthal quantum number and magnetic quantum number are –3.4 eV, 2 and 0 respectively. Which of the following statement(s) is(are) true for the state ψ?
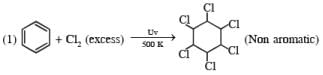
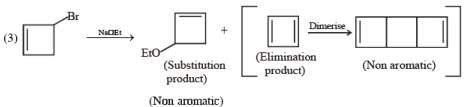
Choose the correct option(s) that give(s) an aromatic compound as the major product.
Consider the following reactions (unbalanced)
Zn + hot conc. H2SO4 → G + R + X
Zn + conc. NaOH → T + Q
G + H2S + NH4OH → Z (a precipitate) + X + Y
Choose the correct option(s).
With reference to aqua regia, choose the correct option(s).
Choose the correct option(s) from the following
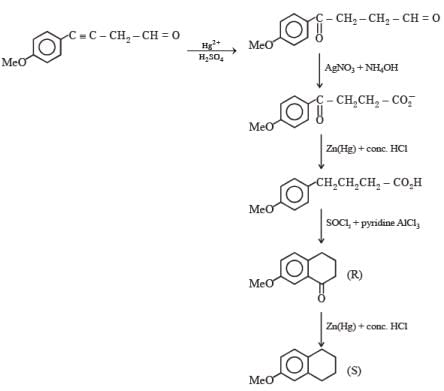
Choose the correct option(s) for the following reaction sequence
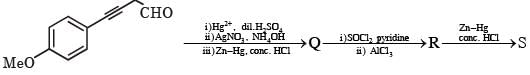
Consider Q, R and S as major products
The decomposition reaction 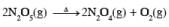 is started in a closed cylinder under isothermal isochoric condition at an initial pressure of 1 atm. After Y × 103 s, the pressure inside the cylinder is found to be 1.45 atm. If the rate constant of the reaction is 5 × 10–4 s–1, assuming ideal gas behavior, the value of Y is ___
is started in a closed cylinder under isothermal isochoric condition at an initial pressure of 1 atm. After Y × 103 s, the pressure inside the cylinder is found to be 1.45 atm. If the rate constant of the reaction is 5 × 10–4 s–1, assuming ideal gas behavior, the value of Y is ___
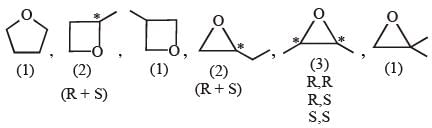
Total number of isomers, considering both structural and stereoisomers, of cyclic ethers with the molecular formula C4H8O is ___
The amount of water produced (in g) in the oxidation of 1 mole of rhombic sulphur by conc.HNO3 to a compound with the highest oxidation state of sulphur is __
(Given data : Molar mass of water = 18 g mol–1)
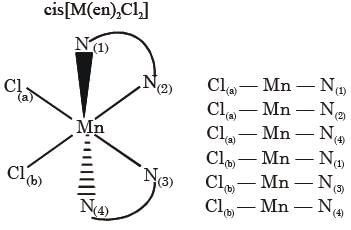
Total number of cis N–Mn–Cl bond angles (that is, Mn–N and Mn–Cl bonds in cis positions) present in a molecule of cis-[Mn(en)2Cl2] complex is ____ (en = NH2CH2CH2NH2)
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


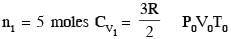
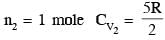
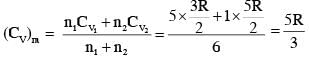
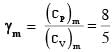
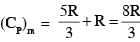
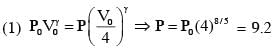 which is between 9P0 and 10P0
which is between 9P0 and 10P0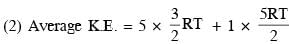
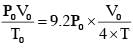
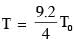
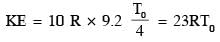
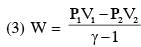
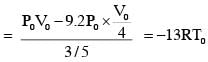
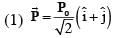
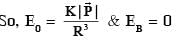

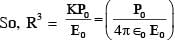
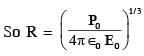
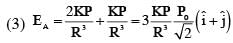
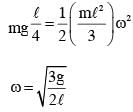
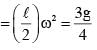
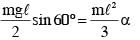
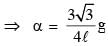
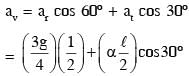
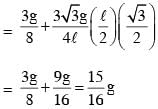
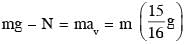
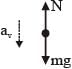
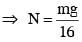

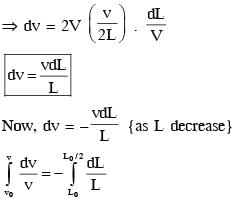
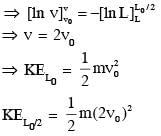
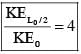
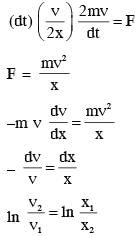
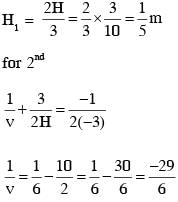
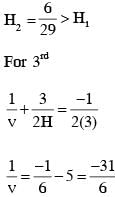
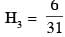
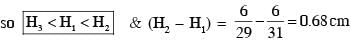
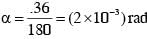
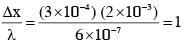
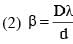
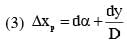
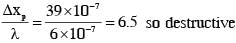
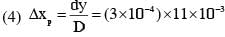


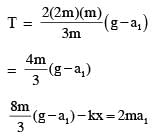
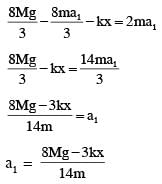
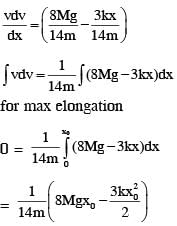
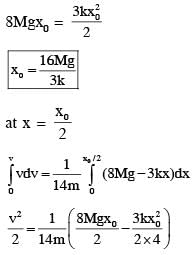
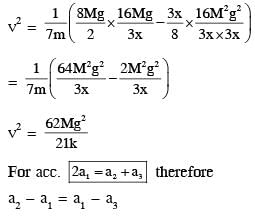
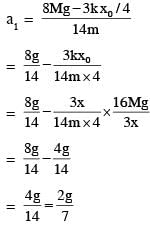
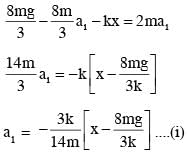
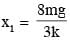 therefore.
therefore.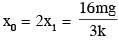
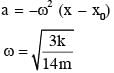
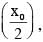 block will be passing through its mean position therefore at mean position
block will be passing through its mean position therefore at mean position