JEE Main 2020 Question Paper with Solution (7th January - Morning) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Main 2020 Question Paper with Solution (7th January - Morning)
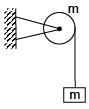
A block of mass m is suspended from a pulley in form of a circular disc of mass m & radius R. The system is released from rest, find the angular velocity of disc when block has dropped by height h. (there is no slipping between string & pulley)

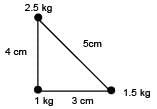
Three point masses 1kg, 1.5 kg, 2.5 kg are placed at the vertices of a triangle with sides 3cm, 4cm and 5cm as shown in the figure. The location of centre of mass with respect to 1kg mass is :

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a single slit diffraction set up, second minima is observed at an angle of 60°. The expected position of first minima is
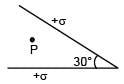
There are two infinite plane sheets each having uniform surface charge density +σ C/m2. They are inclined to each other at an angle 30° as shown in the figure. Electric field at any arbitrary point P is:
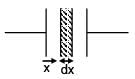
A parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given by k = k0(1 + αx). Calculate capacitance of system: (given αd << 1)
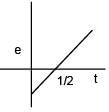
A long solenoid of radius R carries a time dependent current I = I0 t(1 – t). A ring of radius 2R is placed coaxially near its centre. During the time interval 0 ≤ t ≤ 1, the induced current IR and the induced emf VR in the ring vary as:
If 10% of intensity is passed from analyser, then, the angle by which analyser should be rotated such that transmitted intensity becomes zero. (Assume no absorption by analyser and polarizer).
Three moles of ideal gas A with 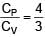 is mixed with two moles of another ideal gas B with
is mixed with two moles of another ideal gas B with 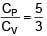 . The
. The 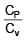 of mixture is (Assuming temperature is constant)
of mixture is (Assuming temperature is constant)
Given magnetic field equation is B = 3 × 10–8 sin(ωt + kx + φ)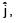 then appropriate equation for electric field (E) will be :
then appropriate equation for electric field (E) will be :
There is a LCR circuit, If it is compared with a damped oscillation of mass m oscillating with force constant k and damping coefficient 'b'. Compare the terms of damped oscillation with the devices in LCR circuit.
A lift can hold 2000kg, friction is 4000N and power provided is 60HP. (1 HP = 746W) Find the maximum speed with which lift can move up.
A H–atom in ground state has time period T = 1.6 × 10–16 sec. find the frequency of electron in first excited state
Magnification of compound microscope is 375. Length of tube is 150mm. Given that focal length of objective lens is 5mm, then value of focal length of eyepiece is:
1 litre of a gas at STP is expanded adiabatically to 3 litre. Find work done by the gas. Given γ = 1.40 and 31.4= 4.65
A string of length 60 cm, mass 6gm and area of cross section 1mm2 and velocity of wave 90m/s. Given young's modulus is Y = 1.6 × 1011 N/m2. Find extension in string.
Which of the following gate is reversible
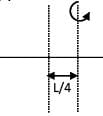
A thin uniform rod is of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance of L/4 from centre and perpendicular to rod.
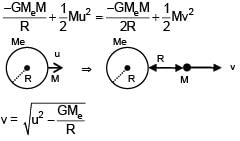
A satellite of mass 'M' is projected radially from surface of earth with speed 'u'. When it reaches a height equal to radius of earth, it ejects a rocket of mass M/10 and itself starts orbiting the earth in circular path
of radius 2R, find the kinetic energy of rocket.
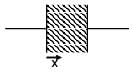
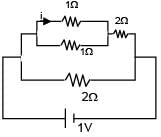
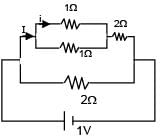
The current 'i' in the given circuit is
A current carrying circular loop is placed in an infinite plane if φ1 is the magnetic flux through the inner region and φ0 is magnitude of magnetic flux through the outer region, then
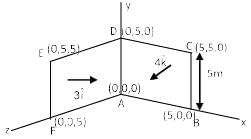
Consider a loop ABCDEFA with coordinates A (0, 0, 0), B(5, 0, 0), C(5, 5, 0), D(0, 5, 0) E(0, 5, 5) and F(0, 0, 5). Find magnetic flux through loop due to magnetic field 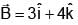
A Carnot's engine operates between two reservoirs of temperature 900K and 300K. The engine performs 1200 J of work per cycle. The heat energy delivered by the engine to the low temperature reservoir in a cycle is:
A non-isotropic solid metal cube has coefficients of linear expansion as 5 × 10–5/°C along the x-axis and 5 × 10–6/°C along y-axis and z-axis. If coefficient of volume expansion of the solid is C × 10–6/°C then the value of C is
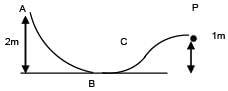
A particle is released at point A. Find its kinetic energy at point P. (Given m = 1 kg and all surfaces are frictionless)
On a photosensitive metal of area 1 cm2 and work function 2eV, light of intensity 6.4 × 10–5 W/cm2 and wavelength 310 nm is incident normally. If 1 out of every 103 photons are successful, then number of photoelectrons emitted in one second is 10x. Find x
Correct order of electron gain enthalpy (kJ/mole) of F, Cl, Br, I
Arrange the following in order of their pKb value
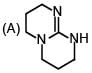 (B) CH3–NH–CH3 (C) CH3–CH=NH
(B) CH3–NH–CH3 (C) CH3–CH=NH
1-Methylethylene oxide 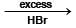 Product 'X' will be –
Product 'X' will be –
Correct order of Intermolecular forces
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


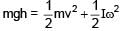
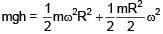
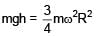
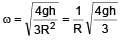
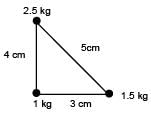
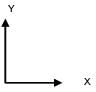
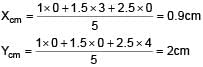
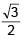 (given)
(given)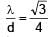 ......(1)
......(1) (from equation (i))
(from equation (i))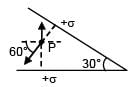
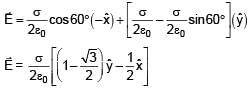
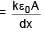
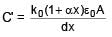
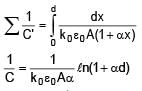
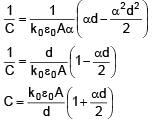
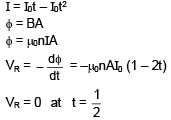
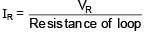
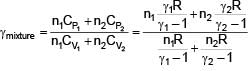
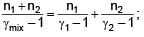
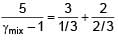
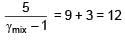
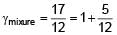
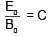 (speed of light in vacuum)
(speed of light in vacuum)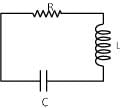
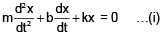
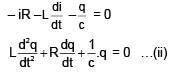
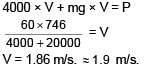
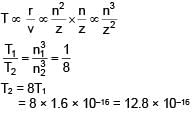
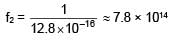
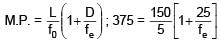
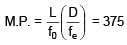
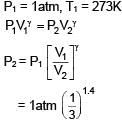
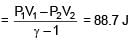
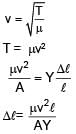
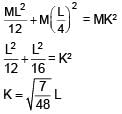

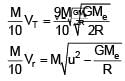
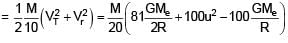
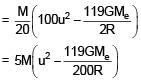
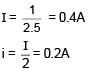
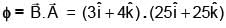

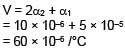
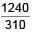 = 4eV > 2eV (so photoelectric effect will take place)
= 4eV > 2eV (so photoelectric effect will take place)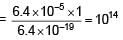
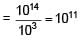
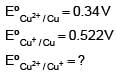
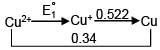
 + 1 x 0.522
+ 1 x 0.522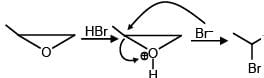 --excess HBr--->
--excess HBr--->