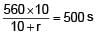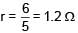JEE Main 2020 Question Paper with Solution (7th January - Evening) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Main 2020 Question Paper with Solution (7th January - Evening)
If weight of an object at pole is 196 N then weight at equator is [g = 10 m/s2 ; radius of earth = 6400 Km]
In a house 15 Bulbs of 45 W, 15 bulbs of 100 W, 15 bulbs of 10 W and Two heaters of 1 KW each is connected to 220 V Mains supply then find minimum fuse current
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In an adiabatic process, volume is doubled then find the ratio of final average relaxation time & initial relaxation time. Given 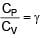
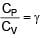
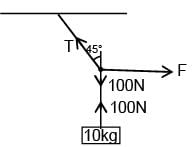
A block of mass 10kg is suspended from string of length 4m. When pulled by a force F along horizontal from midpoint. Upper half of string makes 45° with vertical, value of F is
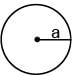
The surface mass density of a disc of radius a varies with radial distance as σ = A + Br where A & B are positive constants then moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane
Cascaded Carnot engine is an arrangement in which heat sink of one engine is source for other. If high temperature for one engine is T1, low temperature for other engine is T2 (Assume work done by both engine is same) Calculate lower temperature of first engine.
Activity of a substance changes from 700 s–1 to 500 s–1 in 30 minute. Find its half-life in minutes
In YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
An ideal fluid is flowing in a pipe in streamline flow. Pipe has maximum and minimum diameter of 6.4 cm and 4.8 cm respectively. Find out the ratio of minimum to maximum velocity.
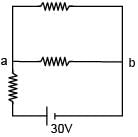
There is a electric circuit as shown in the figure. Find potential difference between points a and b.
A particle of mass m and positive charge q is projected with a speed of v0 in y–direction in the presence of electric and magnetic field are in x–direction. Find the instant of time at which the speed of particle becomes double the initial speed.
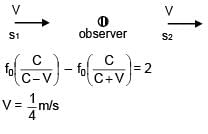
Two sources of sound moving with same speed v and emitting frequency of 1400 Hz are moving such that one source s1 is moving towards the observer and s2 is moving away from observer. If observer hears beat frequency of 2 Hz. Then find the speed of source. Given
Vsound >> VSource
Vsound = 350 m/s
An electron & a photon have same energy E. Find the ratio of de Broglie wavelength of electron to wavelength of photon. Given mass of electron is m & speed of light is C.
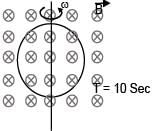
A ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively :
Electric field in space is given by 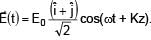 A positively charged particle at (0, 0, π/K) is given velocity v0kˆ at t = 0. Direction of f orce acting on particle is
A positively charged particle at (0, 0, π/K) is given velocity v0kˆ at t = 0. Direction of f orce acting on particle is
Focal length of convex lens in air is 16 cm (μglass = 1.5). Now the lens is submerged in liquid of refractive index 1.42. Find the ratio of focal length in medium to focal length in air has closest value
A lift of mass 920 kg has a capacity of 10 persons. If average mass of person is 68 kg. Friction f orce between lift and lift shaft is 6000 N. The minimum power of motor required to move the lift upward with constant velocity 3 m/s is [g = 10 m/s2]
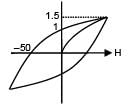
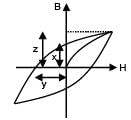
The hysteresis curve for a material is shown in the figure. Then for the material retentivity, coercivity and saturation magnetization respectively will be
An inductor of inductance 10 mH and a resistance of 5Ω is connected to a battery of 20 V at t = 0. Find the ratio of current in circuit at t = ∞ to current at t = 40 sec.
Find the dimension of 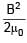
A capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ.
When m gram of steam at 100°C is mixed with 200 gm of ice at 0°C. it results in water at 40°C. Find the value of m in gram .
(given : Latent heat of fusion (Lf) = 80 cal/gm, Latent heat of vaporisation (Lv) = 540 cal/gm., specific heat of water (Cw)= 1 cal/gm/°C)
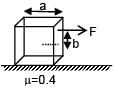
A solid cube of side 'a' is shown in the figure. Find maximum value of 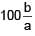 for which the block does
for which the block does
not topple before sliding.
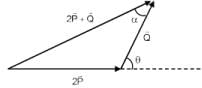
Magnitude of resultant of two vectors  is equal to magnitude of
is equal to magnitude of  . Find the angle between
. Find the angle between 
and resultant of 2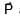 and
and 
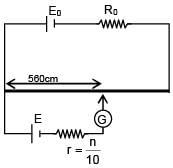
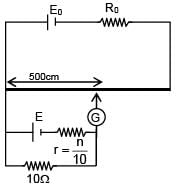
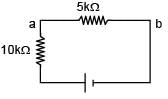
A battery of unknown emf connected to a potentiometer has balancing length 560 cm. If a resistor of resistance 10W is connected in parallel with the cell the balancing length change by 60 cm. If the internal resistance of the cell is n/10 Ω, the value of 'n' is
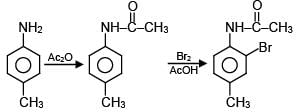
Which of the following reactions are possible?
(A)
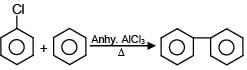
(B)
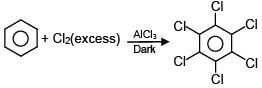
(C)
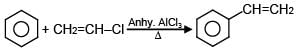
(D)
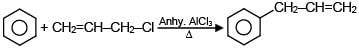
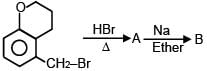
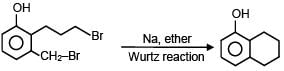
A and B are in the given reaction ?
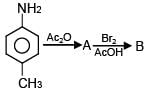
The correct statement about gluconic acid is
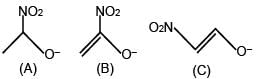
Stability order of following alkoxide ions is
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|





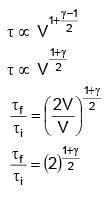

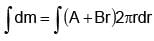

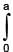 (A + Br )2πr3 dr
(A + Br )2πr3 dr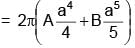
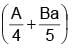
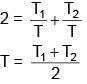
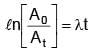
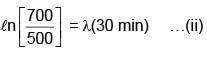
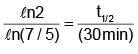
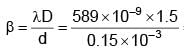
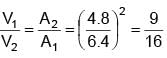
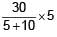 = 10V
= 10V
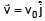 (magnitude of velocity does not change in y–z plane)
(magnitude of velocity does not change in y–z plane)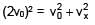
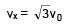
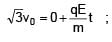
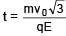
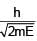
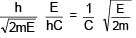
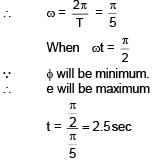
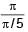 = 5 sec.
= 5 sec.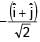

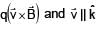

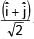
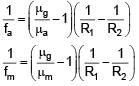
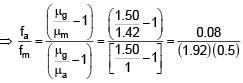
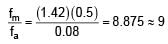
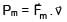
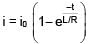

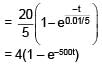
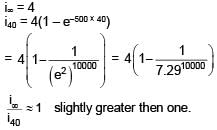
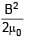

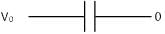
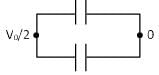
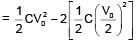
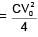
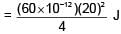
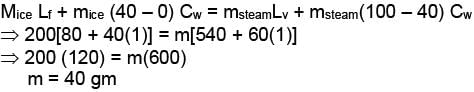
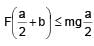
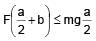
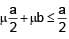
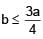
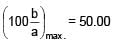
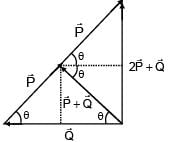
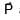 +
+ 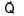 ) and
) and  is 90°
is 90°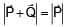

 = ∞
= ∞ ................... (ii)
................... (ii)