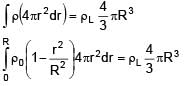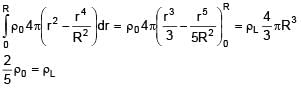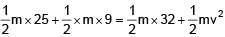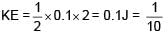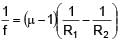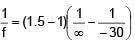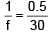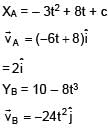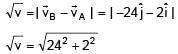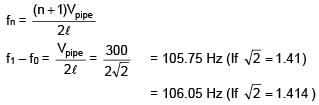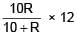JEE Main 2020 Question Paper with Solution (8th January - Morning) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Main 2020 Question Paper with Solution (8th January - Morning)
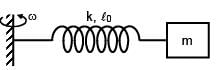
A block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) about the fixed end in gravity free space. The elongation in spring is-
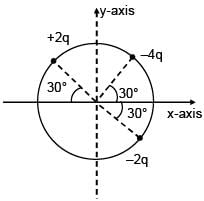
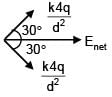
3 point charges are placed on circumference of a circle of radius 'd' as shown in figure. The electric field along x-axis at centre of circle is:

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Choose the correct P-V graph of ideal gas for given V-T graph.

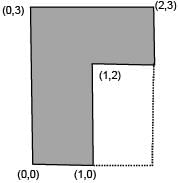
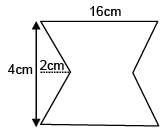
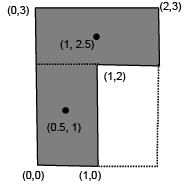
Find the coordinates of centre of mass of the lamina, shown in figure.
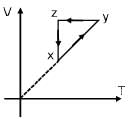
Which graph correctly represents v ariation between relaxation time 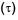 of gas molecules with absolute temperature (T) of an ideal gas.
of gas molecules with absolute temperature (T) of an ideal gas.
If two capacitors C1 & C2 are connected in parallel then equivalent capacitance is 10μF. If both capacitor are connected across 1V battery then energy stored by C2 is 4 times that of C1. Then the equivalent capacitance if they are connected in series is -
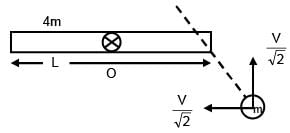
A rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod which is perpendicular to axis of rotation, strikes at one end at an angle of 45º and sticks to it. The angular velocity of system after collision is–
Two photons of energy 4eV and 4.5eV are incident on two metals A and B respectively. Maximum kinetic energy for ejected electron is TA for A and TB = TA – 1.5eV for metal B. Relation between de-Broglie wavelengths of ejected electron of A and B are λB = 2λA. The work function of metal B is -
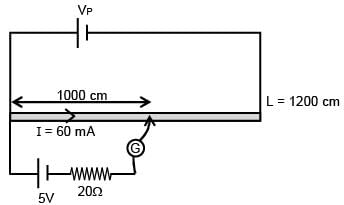
There is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20Ω is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is–
A telescope has magnifying power 5 and length of tube is 60cm then the focal length of eye piece is–
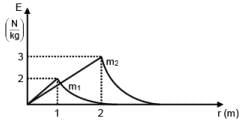
Two spherical bodies of mass m1 and m2 have radii 1 m and 2 m respectively. The gravitational field of the two bodies with the radial distance from centre is shown below. The value of 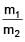 is-
is-
When a proton of KE = 1.0 MeV moving in South to North direction enters the magnetic field (from West to East direction), it accelerates with acceleration a = 1012 m/s2. The magnitude of magnetic field is–
If electric field around a surface is given by 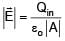 where 'A' is the normal area of surface and Qin is the charge enclosed by the surface. This relation of gauss's law is valid when
where 'A' is the normal area of surface and Qin is the charge enclosed by the surface. This relation of gauss's law is valid when
Stopping potential depends on Planks constant (h), current (I), Universal gravitational constant (G) and speed of light (C). Choose the correct option for the dimension of stopping potential (V)
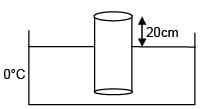
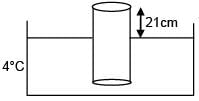
A cylinder of height 1m is floating in water at 0°C with 20 cm height in air. Now temperature of water is raised to 4°C, height of cylinder in air becomes 21cm. The ratio of density of water at 4°C to density of water at 0°C is– (Consider expansion of cylinder is negligible)
Number N of the α-particles deflected in Rutherford's α-scattering experiment varies with the angle of deflection θ. Then the graph between the two is best represented by.
If relative permittivity and relative permeability of a medium are 3 and 4/3 respectively. The critical angle for this medium is.
The given loop is kept in a uniform magnetic field perpendicular to plane of loop. The field changes from 1000G to 500G in 5seconds. The average induced emf in loop is–
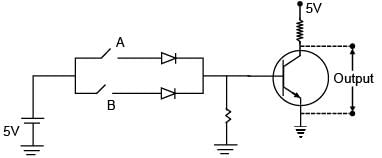
Choose the correct Boolean expression for the given circuit diagram:
A solid sphere of density 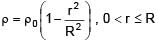 just floats in a liquid. The density of liquid is –
just floats in a liquid. The density of liquid is –
(r is distance from centre of sphere)
Two particles each of mass 0.10kg are moving with velocities 3m/s along x-axis and 5m/s along y-axis respectively. After an elastic collision one of the mass moves with a velocity 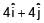 . The energy of other particle after collision is x/10 , then x is.
. The energy of other particle after collision is x/10 , then x is.
A plano-convex lens of radius of curvature 30 cm made of refractive index 1.5 is kept in air. Find its focal length (in cm).
Position of two particles A and B as a function of time are given by XA = – 3t2 + 8t + c and YB = 10 – 8t3. The velocity of B with respect to A at t = 1 is √v . Find v.
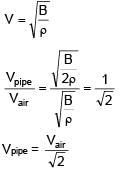
An open organ pipe of length 1m contains an ideal gas whose density is twice the density of atmosphere at STP. Find the difference between fundamental and second harmonic frequencies if speed of sound in atmosphere is 300 m/s.
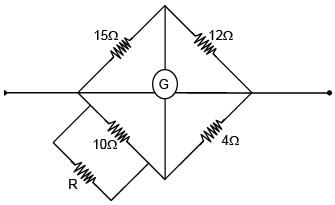
Four resistors of 15Ω, 12Ω, 4Ω and 10Ω are arranged in cyclic order to form a wheatstone bridge. What resistance (in Ω) should be connected in parallel across the 10Ω resistor to balance the wheatstone bridge.
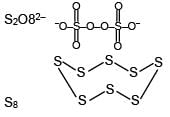
Number of S–O bond in S2O82– and number of S–S bond in Rhombic sulphur are respectively:
Following vanderwaal forces are present in ethyl acetate liquid
Given, for H-atom
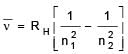
Select the correct options regarding this formula for Balmer series.
Correct order of first ionization energy of the following metals Na, Mg, Al, Si in KJ mol-1 respectively are:
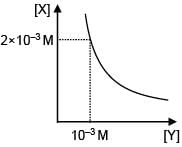
Select the correct stoichiometry and its ksp value according to given graphs.
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


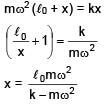
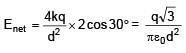
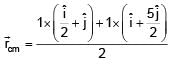
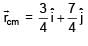
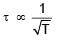

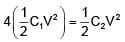
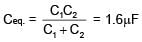
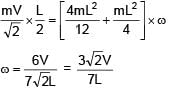
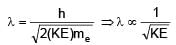
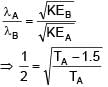
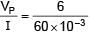 = 100Ω
= 100Ω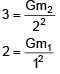
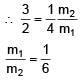
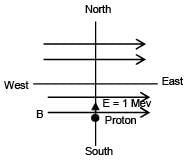
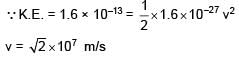 ∴ Bqv = ma
∴ Bqv = ma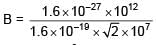
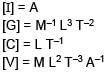
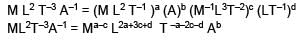
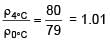
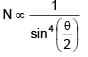
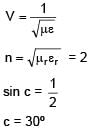
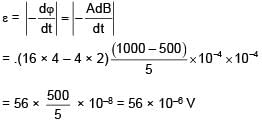
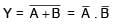
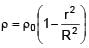 0 < r ≤ R
0 < r ≤ R