Test: 35 Year JEE Previous Year Questions: Circle - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - Test: 35 Year JEE Previous Year Questions: Circle
A triangle with vertices (4, 0), (–1, –1), (3, 5) is
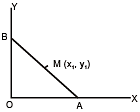
Locus of mid point of the portion between the axes of x cosα + y sina = p whre p is constant is [2002]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the pair of lines ax2+2hxy+by2+2gx+2fy+c=0 intersect on the y-axis then [2002]
The pair of lines represented by 3ax2 + 5xy + (a2 – 2)y2 = 0 are perpendicular to each other for [2002]
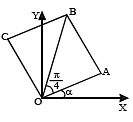
A square of side a lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle  with the positive direction of x-axis. The equation of its diagonal not passing through the origin is
with the positive direction of x-axis. The equation of its diagonal not passing through the origin is
If the pair of straight lines x2 - 2 pxy - y2 = 0 and x2 - 2qxy -y2=0 be such that each pair bisects the angle between the other pair, then [2003]
Locus of centroid of the triangle whose vertices are (a cos t, a sin t ), (b sin t, - b cos t ) and (1, 0), where t is a parameter, is [2003]
If x1, x2 , x3 and y1, y2,y3 are both in G.P. with the same common ratio, then the points ( x1, y1), (x2 , y2) and (x3 , y3) [2003]
If the equation of the locus of a point equidistant from the point (a1, b1) and (a2, b2) is (a1 -b2) x + (a1 -b2) y + c= 0 , then the value of `c` is [2003]
Let A(2, - 3) and B ( -2, 3) be vertices of a triangle ABC. If the centroid of this triangle moves on the line 2x + 3y= 1, then the locus of the vertex C is the line
The equation of the straight line passing th rough the point (4, 3) and making intercepts on the co-ordinate axes whose sum is –1 is [2004]
If the sum of t he slopes of the lines given by x2 - 2cxy - 7y2 = 0 is four times their product c has the value[2004]
If one of the lines given by 6x2 - xy + 4cy2 = 0 is 3x + 4y = 0, then c equals [2004]
The line parallel to the x- axis and passing through the intersection of the lines ax + 2by + 3b = 0 and bx – 2ay – 3a = 0, where (a, b) ≠ (0, 0) is [2005]
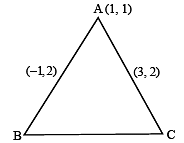
If a vertex of a triangle is (1, 1) and the mid points of two sides through this vertex are (–1, 2) and (3, 2) then the centroid of the triangle is [2005]
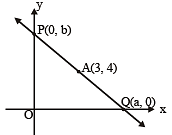
A straight line through the point A (3, 4) is such that its intercept between the axes is bisected at A. Its equation is
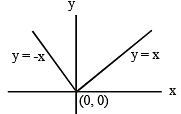
If (a,a2) falls inside the angle made by the lines y = 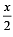 x > 0 and y = 3x , x > 0 , then a belong to [2006]
x > 0 and y = 3x , x > 0 , then a belong to [2006]
Let A (h, k), B(1, 1) and C (2, 1) be the vertices of a right angled triangle with AC as its hypotenuse. If the area of the triangle is 1square unit, then the set of values which 'k' can take is given by [2007]
Let P = (–1, 0), Q = (0, 0) and R = (3,  ) be three point. The equation of the bisector of the angle PQR is [2007]
) be three point. The equation of the bisector of the angle PQR is [2007]
If one of the lines of my2 + (1– m2) xy – mx2 = 0 is a bisector of the angle between the lines xy = 0, then m is [2007]
The perpendicular bisector of the line segment joining P (1, 4) and Q(k, 3) has y-intercept –4. Then a possible value of k is[2008]
The shortest distance between the line y – x = 1 and the curve x = y2 is : [2009]
The lines p(p2 +1)x – y + q = 0 and (p2 + 1)2x + (p2 + 1)y + 2q = 0 are perpendicular to a common line for : [2009]
Three distinct points A, B and C are given in the 2-dimensional coordinates plane such that the ratio of the distance of any one of them from the point (1, 0) to the distance from the point (–1, 0) is equal to 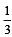 . Then the circumcentre of the triangle ABC is at the point: [2009]
. Then the circumcentre of the triangle ABC is at the point: [2009]
The line L given by 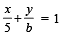 passes through the point (13, 32). The line K is parallel to L and has the equation
passes through the point (13, 32). The line K is parallel to L and has the equation 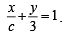 Then the distance between L and K is [2010]
Then the distance between L and K is [2010]
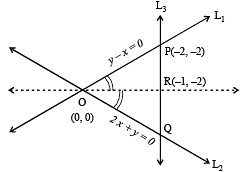
The lines L1 : y – x = 0 and L2 : 2x + y = 0 intersect the line L3 : y + 2 = 0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R.
Statement-1: The ratio PR : RQ equals 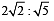
Statement-2: In any triangle, bisector of an angle divides the triangle into two similar triangles. [2011]
If the line 2x + y = k passes through the point which divides the line segment joining the points (1,1) and (2,4) in the ratio 3 :2, then k equals : [2012]
A ray of light along 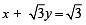 gets reflected upon reaching x-axis, the equation of the reflected ray is [JEE M 2013]
gets reflected upon reaching x-axis, the equation of the reflected ray is [JEE M 2013]
The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1) (1, 1) and (1, 0) is : [JEE M 2013]
Let PS be the median of the triangle with vertices P(2, 2), Q(6, –1) and R(7, 3). The equation of the line passing through (1, –1) and parallel to PS is: [JEE M 2014]
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


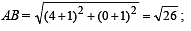
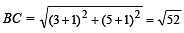
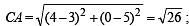
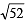 or BC2 = 52
or BC2 = 52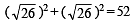
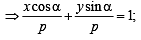
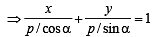
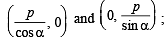
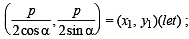
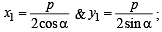
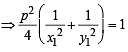

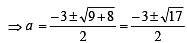
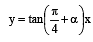
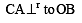
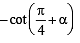

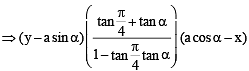


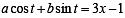
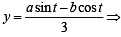

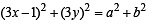
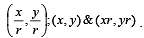
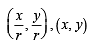
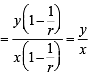
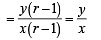 ∴ m1 = m2
∴ m1 = m2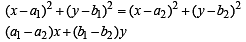
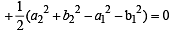
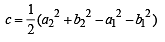

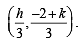 It lies on 2x + 3y = 1
It lies on 2x + 3y = 1 .
.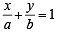 ......(1)
......(1)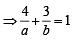
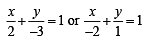
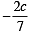 and 4 m1m2 =
and 4 m1m2 = 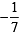
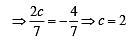
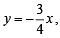
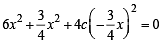
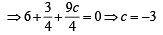
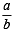 (bx – 2ay – 3a) = 0
(bx – 2ay – 3a) = 0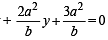
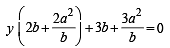

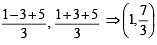
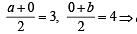 a = 6, b = 8
a = 6, b = 8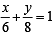 or 4x + 3y = 24
or 4x + 3y = 24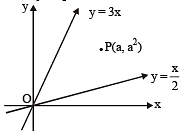
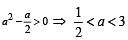
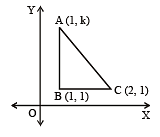
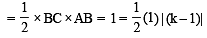
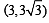 respectively..
respectively..
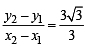

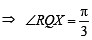
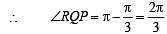
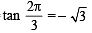
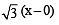
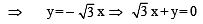
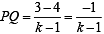
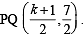

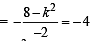
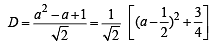
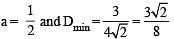
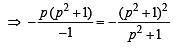
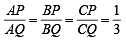
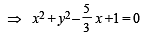 ....(1)
....(1)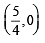
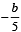
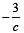

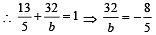
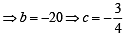
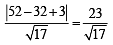

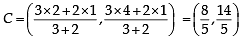
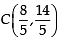
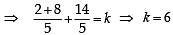
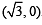 So, equation of
So, equation of

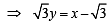
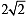 , c = 2
, c = 2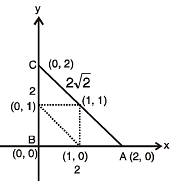
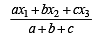
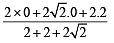
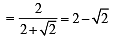
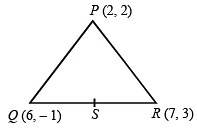
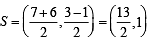

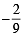 is
is