Olympiad Test: Understanding Quadrilaterals
20 Questions MCQ Test Mathematics (Maths) Class 8 | Olympiad Test: Understanding Quadrilaterals
| 1 Crore+ students have signed up on EduRev. Have you? |
ABCD is a quadrilateral. If AC and BD bisect each other, what is ABCD?
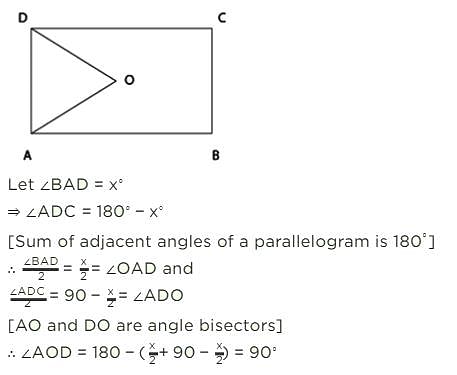
ABCD is a parallelogram. The angle bisectors of ∠A and ∠D meet at O. What is the measure of ∠AOD?
The diagonal of a rectangle is 10 cm and its breadth is6 cm. What is its length?
Apply Pythagoras Theorem,
(Diagonal)2 = (Breadth)2 + (Length)2
100 = 36+(Length)2
Length=8cm
ABCD and MNOP are quadrilaterals as shown in the figure.
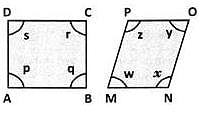
Which of the following is correct?
What do you call a parallelogram which has equal diagonals?
In a square ABCD, the diagonals bisect at O. What type of a triangle is AOB?
Since diagonals of a square are equal and bisect at right angles, triangle AOB is an isosceles right angled triangle.
The perimeter of a parallelogram is180 cm. If one side exceeds the other by 10 cm, what are the sides of the parallelogram?
Let one side of the parallelogram be 'x' cm. Then adjacent side is (x+10)cm.
∴ Perimeter = x+(x+10)+x+(x+10) = 180
(Given) ⇒ 4x+20 = 180 or x = 40cm
∴ x+10 = 50cm
In the quadrilateral ABCD, the diagonals AC and BD are equal and perpendicular to each other. What type of a quadrilateral is ABCD?
A quadrilateral in which the diagonals are equal and perpendicular is called a square.
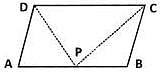
ABCD is a parallelogram as shown in the figure. If AB = 2AD and P is the mid-point of AB, what is the measure of ∠CPD ?
As shown in the figure, since P is the midpoint of AB and AB = 2AD,we have AB = 2AP = 2AD or AP = AD. i.e.,
triangle ADP is an isosceles triangle. If ∠ADP = xo and ∠APD = xo, then ∠A = 180o−2xo.
Since ∠B is adjacent to ∠A, in ABCD ∠B = 180o−(180o−2x) = 2x. In ΔCBP,xo+xo+2xo = 180o(Angle sum property)
⇒ 4xo = 180o ⇒ xo = 45o ∴∠CPD = 180o−2xo = 180o−2×45o = 90o
In a parallelogram ABCD, if AB = 2x+5, CD = y+1, AD= y+5 and BC = 3x−4,what is the ratio of AB and BC?
We know that in a parallelogram opposite sides are equal.
∴ AB = CD or 2x+5=y+1 and
AD = BC or y+5=3x−4
2x−y =−4 ....(i)
y−3x = −9 .....(ii)
Adding (i) and (ii),
we get −x =−13 or x = 13
and y = 30.
Substituting, we have
AB = 31 cm and BC = 35 cm
∴The required ratio = 31:35
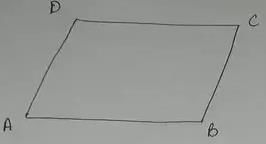
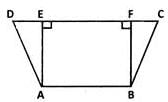
If ABCD is an isosceles trapezium, what is the measure of ∠C?
From definition, we know that in an isosceles trapezium the non-parallel sides are equal or AD = BC in the figure. Drop perpendiculars AE and BF to CD. Triangles AED and BFC are congruent by R.H.S congruency. Hence, ∠D = ∠C
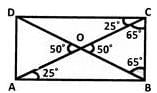
A diagonal of a rectangle is inclined to one side of the rectangle at 25o. What is the measure of the acute angle between the diagonals?
Since ∠CAB = 25o ∠CAB = 65o
Let diagonals meet at O. ΔOCB is an isosceles triangle.
∴ ∠OBC = 65o
⇒ ∠BOC = 50o
If angles P, Q, R and S of the quadrilateral PQRS, taken in order, are in the ratio 3:7:6:4, what is PQRS?
Let the angles be 3x, 7x , 6x and 4x.
∴ 3x+7x+6x+4x = 360o or 20x = 360o or x = 18o.
The angles are 54o,126o,108o and 72o.
We see that adjacent angles are supplementary but opposite angles-are not equal. Clearly, it is a trapezium.
If AB and CD are diameters, what is ACBD?
Since the angle in a semicircle is a right angle, clearly ∠A = ∠C = ∠B = ∠D = 90o
The diagonals (diameters) are equal but they are not intersecting (bisecting) at right angles. Hence, it is not a square and can be only a rectangle.
If two adjacent angles of a parallelogram are in the ratio 3:2, what are their measures?
Let the angles be 3x and 2x. We have, 3x+2x = 180o ⇒ 5x = 180o ⇒ x = 36o
∴ The angles are 36o×3 and 36o×2 = 108o and 72o.
ABC and DEF are straight lines.
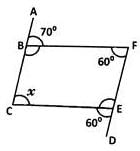
Find the value of 'x',
In the given figure. ∠ABF+∠FBC = 180o.
70o+∠FBC = 180o ⇒ ∠FBC = 180o−70o = 110o
Now, ∠DEC+∠CEF = 180o
∠CEF = 180o−60o = 120o
Now, ∠FBC+∠BCE+∠CEF+∠BFE = 36o
290o+x = 360o ⇒ x = 70o
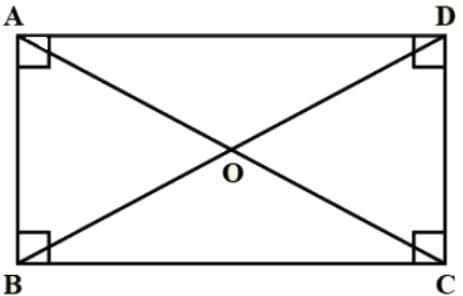
ABCD is a rectangle. Its diagonals meet at O.
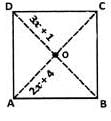
Find x; if OA = 2x+4 and OD = 3x+1.
OD is half of the diagonal BD and OA is half of the diagonal AC. Diagonals are equal. So, their halves are also equal. Therefore, 3x + 1 = 2x + 4
⇒ x = 3.
ABCD is a rhombus.
Find the respective values of x, y and z.
x = OB = OD (Diagonals bisect) = 5
y = OA = OC (Diagonals bisect) = 12
z = side of the rhombus = 13 (All sides are equal).
In the figure, ABCD is a parallelogram.
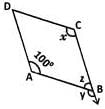
Find the respective values of x, y and z.
C is opposite to A. So,
x = 100o (Opposite angles property.)
y = 100o (Measure of angle corresponding to ∠x.)
z = 80o (Since ∠y,∠z is a linear pair)
In the figure, ABCD is a rhombus and ABDE is a parallelogram.
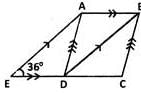
Given that EDC is a straight line and ∠AED = 36o find ∠BAD.
BDC = AED = 36o (Corresponding s, AE BD.) ABD= BDC = 36o (Alternate s, AB DC) ADB = ABD = 36o (Base angles of isosceles, since AB = DC) BAD = 180o−ABD−ADB (Angle sum of a triangle.) = 180o−36o−36o = 108o
|
193 videos|360 docs|48 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
193 videos|360 docs|48 tests
|
Download free EduRev App
Related content with Olympiad Test: Understanding Quadrilaterals
|
|
|
|
Related tests with Olympiad Test: Understanding Quadrilaterals
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
