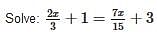Courses

Test: Linear Equations- 2


20 Questions MCQ Test Mathematics (Maths) Class 8 | Test: Linear Equations- 2


Description
This mock test of Test: Linear Equations- 2 for Class 8 helps you for every Class 8 entrance exam. This contains 20 Multiple Choice Questions for Class 8 Test: Linear Equations- 2 (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Linear Equations- 2 quiz give you a good mix of easy questions and tough questions. Class 8 students definitely take this Test: Linear Equations- 2 exercise for a better result in the exam. You can find other Test: Linear Equations- 2 extra questions, long questions & short questions for Class 8 on EduRev as well by searching above.
QUESTION: 1

Solve: 4y = 20

Solution: 4y = 20 y = 20/4 y = 5
QUESTION: 2

Solve: 3x = 2x+ 18

Solution: 3x=2x+18 3x-2x=18 (transposing) x= 18
QUESTION: 3

Solve: x = 4/5(x+10)

Solution:
x = 4/5*(x + 10)
=> x = 4x/5 + 8
=> x - 4x/5 = 8
=> (5x - 4x)/5 = 8
=> x = 8 * 5 = 40
Verification / Checking-
LHS = x = 40
RHS = 4/5*(x + 10) = 4/5*(40 + 10) = 4/5 * 50 = 40
QUESTION: 4

The sum of three consecutive multiples of 7 is 357. Find the smallest multiple.
Solution:
QUESTION: 5

In an equation the values of the expressions on the LHS and RHS are _______.
Solution:
QUESTION: 6

The sum of two digits and the number formed by interchanging its digit is 110. If ten is subtracted from the first number, the new number is 4 more than 5 times of the sum of the digits in the first number. Find the first number.       
Solution:

Let the unit digit be y & tens digit be x.

Original number = (10x+y)

After interchanging the digits 

New number = (10y+x)

(10x+y) + (10y+x) = 110

11x +11y = 110

11(x+y)= 110

x+y = 110/11

x+y= 10          (1)

x= 10-y           (2)

(10x+y) - 10 = 4+ 5(x+y)

(10x+y) - 10 = 4+ 5(10)

(10x+y) = 4+ 50+10

(10x+y) = 64

10(10-y) +y = 64

100-10y +y= 64

100 -9y = 64

-9y = 64-100

-9y = -36

y= 36/9= 4

y= 4

putting the value of y in eqn 2

x= 10-y

x= 10-4

x= 6

Hence , the first number is 6 & second number is 4.

Original Number is 10x+y = 10* 6+4= 60+4= 64

QUESTION: 7

Solve: x − 2 = 7
Solution:
QUESTION: 8

Solve: 5t – 3 = 3t – 5
Solution:

5t-3=3t-55t-3t=-5+32t=-2 which gives t=-1

QUESTION: 9

What will be the solution of these equations ax+by = a-b, bx-ay = a+b       
Solution:

ax+by=a-b
ax=a-b-by
x=(a-b-by)/a
bx-ay=a+b
substituting
b((a-b-by)/a)-ay=a+b
(ab-b²-b²y-a²y)/a=a+b
ab-b²-(b²+a²)y=a²+ab
-(b²+a²)y=a²+ab-ab+b²
y=-(a²+b²)/(a²+b²)
y= -1
substituting value of y
x=(a-b-b(-1))/a
x=a/a
x=1

QUESTION: 10

The present age of Sahil’s mother is three times the present age of Sahil. After 5 years their ages will add to 66 years. Find their present ages.
Solution:
Let present age of sahil is 'x'
his mother age is '3x'
after five yearssahil's age is 'x+5'
his mother's age is '3x+5'
according to problem, given sum of their ages after five years is 66
⇒(x+5)+(3x+5)=66
4x+10=664x=66-10
4x=56
x=56/4
x=14sahil's age is x=14=14 years
sahil's mother age is 3x=3(14)= 42=42 years.
QUESTION: 11

Amina thinks of a number and subtracts 5/2 from it. She multiplies the result by 8. The result now obtained is 3 times the same number she thought of. What is the number?
Solution:
Let she thoughts the no x
according to question ,she subtract the 5/2 from the no.= x-5/2
now ,she multiply the result by 8 =8(x-5/2)
according to statement
3x = 8(x-5/2)
3x=8x -20
20=5x
x=4
she thought the no. as 4
QUESTION: 12

Solve: 7x = 21
Solution:
QUESTION: 13

Solve: 5x+ 9 = 5 + 3x
Solution:
QUESTION: 14

Solve: y + 3 = 10
Solution: Option B is correct bcoz...
y + 3 = 10
y = 10 - 3
y = 7
QUESTION: 15

Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Solution:

Let the number be x.
So, the other number is (x + 15).
(x + 15) + x = 95
2x + 15 = 95
2x = 95 - 15
2x = 80
x = 40
So, the numbers are 40 and 55.

QUESTION: 16

The value of the expression on one side of the equality sign is _____ to the value of the expression on the other side.
Solution:

This says that any given equation says that it’s LHS is equal to RHS.

QUESTION: 17

Solution: 2x/3 + 1 = 7x/15 + 3 => 2x/3 -- 7x/15 = 3 -- 1 => 10x -- 7x/15 = 2 => 3x/15 = 2 => 3x = 2 × 15 => 3x = 30 => x = 30/3 => x = 10
QUESTION: 18

Solve: 5a = 30
Solution:
QUESTION: 19

Arjun is twice as old as Shriya. Five years ago his age was three times Shriya’s age. Find their present ages.
Solution:
Let Arjun's age be x and shriya's age be y
A.T.Q.
x=2y
x-5=3 (y-5)
=>x-5=3y-15
=>2y-3y=-15+5
=>-y=-10
=>y=10 
Now ,
x=2y
=>x=(2x10)
=>x=20
Therefore Arjun's age is 20 yrs and Shriya's age is 10 yrs.
QUESTION: 20

8 men and 12 boys can finish a piece of work in 10 days while 6 men and 8 boys can finish the work in 14 days. find the time taking by 1 man alone and 1 boy alone to finish the same work.
Solution:

Let the time taken by man be x days

time taken by boys be y days

work done by 1 man in one day=1/x

work done by 1 boy in one day=1/y

8/x+12/y = 1/10     - eq 1

6/x+ 8/y = 1/14       - eq2

Let u = 1/x & v = 1/y

8u+ 12y = 1/10       - eq3

6u+8v = 1/14         - eq4

Multiplying eq3 by 2 & eq4 by 3 

16u+ 24y = 2/10    - eq5
18u+24v = 3/14      - eq6

subtract eq 5 & 6
-2u = -3/14+2/10
-2u = (-3×10 +2×14)/140

-2u = (-30+28)/140

-2u = -2/140

u = 1/140

put this value in eq 5

16u+ 24y = 2/10

16×1/140 +24y  = 1/5

4/35+24y = 1/5

24y = 1/5-4/35

24y = (1×7-4)/35

24y = (7-4)/35

24y = 3/35

y= 3/35×24

y= 1/280

u=1/x

1/140 = 1/x

x = 140

v = 1/y

1/280 = 1/y
y = 280

A man complete the work in 140 days
A boy can complete the work in 280 days

Recommended Content

Recommended Tests

Similar Content

Related tests

Follow Us
© 2015-20 EduRev