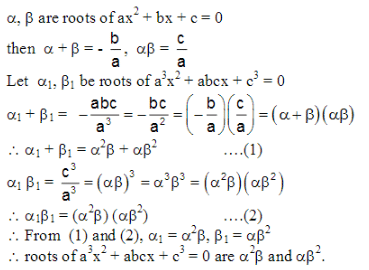Polynomials - Olympiad Level MCQ, Class 10 Mathematics - Class 10 MCQ
30 Questions MCQ Test Extra Documents, Videos & Tests for Class 10 - Polynomials - Olympiad Level MCQ, Class 10 Mathematics
If α,β and γ are the zeros of the polynomial 2x3 – 6x2 – 4x + 30, then the value of (αβ + βγ + γα) is
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If x + 2 is a factor of x3 – 2ax2 + 16, then value of a is
If α,β and γ are the zeros of the polynomial f(x) = x3 + px2 – pqrx + r, then 
=
If the parabola f(x) = ax2 + bx + c passes through the points (–1, 12), (0, 5) and (2, –3), the value of a + b + c is –
If a, b are the zeros of f(x) = x2 + px + 1 and c, d are the zeros of f(x) = x2 + qx + 1 the value of E = (a – c) (b – c) (a + d) (b + d) is –
If α,β are zeros of ax2 + bx + c then zeros of a3x2 + abcx + c3 are –
Let α,β be the zeros of the polynomial x2 – px + r and 
be the zeros of x2 – qx + r. Then the value
of r is –
When x200 + 1 is divided by x2 + 1, the remainder is equal to –
If a (p + q)2 + 2bpq + c = 0 and also a(q + r)2 + 2bqr + c = 0 then pr is equal to –
If a,b and c are not all equal and α and β be the zeros of the polynomial ax2 + bx + c, then value of (1 + α + α2) (1 + β + β2) is :
Two complex numbers α and β are such that α + β = 2 and α4 + β4 = 272, then the polynomial whose zeros
are α and β is –
If 2 and 3 are the zeros of f(x) = 2x3 + mx2 – 13x + n, then the values of m and n are respectively –
If α,β are the zeros of the polynomial 6x2 + 6px + p2, then the polynomial whose zeros are (α + β)2 and (α - β)2 is
If c, d are zeros of x2 – 10ax – 11b and a, b are zeros of x2 – 10cx – 11d, then value of a + b + c + d is –
If the ratio of the roots of polynomial x2 + bx + c is the same as that of the ratio of the roots of x2 + qx + r, then –
If the roots of the polynomial ax2 + bx + c are of the form 
and 
then the value of (a + b + c)2 is–
If α, β and γ are the zeros of the polynomial x3 + a0x2 + a1x + a2, then (1 – α2) (1 – β2) (1 – γ2) is
If α,β,γ are the zeros of the polynomial x3 – 3x + 11, then the polynomial whose zeros are (α + β), (β + γ) and
(γ + α) is –
If α,β,γ are such that α + β + γ = 2, α2 + β2 + γ2 = 6, α3 + β3 + γ3 = 8, then α4 + β4 + γ4 is equal to–
If α,β are the roots of ax2 + bx + c and α + k, β + k are the roots of px2 + qx + r, then k =
If α,β are the roots of the polynomial x2 – px + q, then the quadratic polynomial, the roots of which are (α2– β2) (α3 – β3) and (α3β2 + α2β3) :
The condition that x3 – ax2 + bx – c = 0 may have two of the roots equal to each other but of opposite signs is:
If the roots of polynomial x2 + bx + ac are α,β and roots of the polynomial x2 + ax + bc are α,γ then the values of α,β,γ respectively are –
If one zero of the polynomial ax2 + bx + c is positive and the other negative then (a,b,c εR, a = 0)
If α,β are the zeros of the polynomial x2 – px + q, then 
is equal to –
If α,β are the zeros of the polynomial x2 – px + 36 and α2 + β2 = 9, then p =
If α,β are zeros of ax2 + bx + c, ac = 0, then zeros of cx2 + bx + a are –
A real number is said to be algebraic if it satisfies a polynomial equation with integral coefficients. Which of the following numbers is not algebraic :
The bi-quadraic polynomial whose zeros are 1, 2, 4/3, - 1 is :
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|
Top Courses for Class 10
Important Questions for Polynomials - Olympiad Level MCQ, Class 10 Mathematics
Polynomials - Olympiad Level MCQ, Class 10 Mathematics
Online Tests for Polynomials - Olympiad Level MCQ, Class 10 Mathematics Extra Documents, Videos & Tests for Class 10
|
© EduRev
|
Education Revolution
|
|
