Test: Triangles- 2 - Class 9 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Triangles- 2
In ΔABC, AB = 2.5 cm and BC = 6 cm. Then, the length of AC cannot be
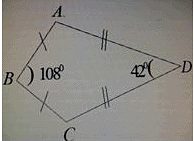
In figure, ABCD is a quadrilateral in which AB = BC and AD = DC. Measure of ∠BCD is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the adjoining figure, △ABC ≅ △ADC. If ∠BAC = 30∘ and ∠ABC = 100∘ then ∠ACD is equal to
It is not possible to construct a triangle when the lengths of its sides are
In triangles ABC and DEF, AB = FD and ∠A=∠D. The two triangles will be congruent by SAS axiom if :
D is a Point on the Side BC of a △ABC such that AD bisects ∠BAC then:
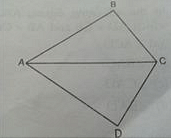
In the adjoining figure, O is Mid – point of AB. If ∠ACO = ∠BDO, then ∠OAC is equal to
In the adjoining fig, AD = BC and ∠BAD = ∠ABC. If ∠BAD = 120∘ and ∠ABD = 35∘, then ∠CAD is
In △ABC, ∠A = 35∘ and ∠B = 65∘, then the longest side of the triangle is:
In △ABC, if ∠A = 45∘ and ∠B = 70∘, then the shortest and the longest sides of the triangle are respectively,
In the adjoining figure, AB = BC and ∠ABD = ∠CBD, then another angle which measures 30∘ is
ABC ≅ △PQR. If AB=5 cm, and ∠A = 60ο then which of the following is true?
In fig., △ABD ≅ △ACD, AB = AC, name the criteria by which the triangles are congruent:
P is a point on side BC of a △ABC such that AP bisects △BAC. Then
In the adjoining figure, AC = BD. If ∠CAB = ∠DBA, then ∠ACB is equal to
In △ABC, if ∠B = 30∘ and ∠C = 70∘, then which of the following is the longest side?
In the adjoining fig, PQ = PR. If ∠QPR = 48∘, then value of x is:
In the adjoining figure, ABCD is a quadrilateral in which AD = CB and AB = CD, then ∠ACB is equal to
In the adjoining figure, PQ > PR. If OQ and OR are bisectors of ∠Q and ∠R respectively, then
In the adjoining fig, AD = BC and ∠BAD = ∠ABC. If ∠BAD = 120∘ and ∠ABD = 35∘, then ∠CAD is
|
44 videos|412 docs|55 tests
|
|
44 videos|412 docs|55 tests
|