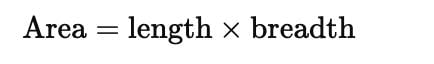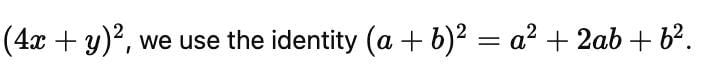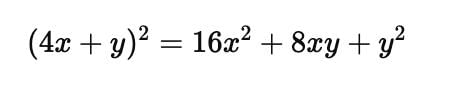Get the App Signup / Login
Sign in Open App

Test: Algebraic Expressions And Identities- 2


40 Questions MCQ Test NCERT Mathematics for CAT Preparation | Test: Algebraic Expressions And Identities- 2


Description
Attempt Test: Algebraic Expressions And Identities- 2 | 40 questions in 40 minutes | Mock test for Class 8 preparation | Free important questions MCQ to study NCERT Mathematics for CAT Preparation for Class 8 Exam | Download free PDF with solutions
QUESTION: 1

The number of terms in the expression 2x2+3x+5 is

Solution:

Yes 3 as the terms are 2x2 ,3x, 5

QUESTION: 2

The coefficient of x in the expression -7x +5 is

Solution:
QUESTION: 3

The numerical coefficient of y in the expression 2x+3y+7z is

Solution:

Since the expression 2x+3y+7z cannot be added as they have different variables so the coefficient of y is 3 only.

QUESTION: 4

The expression y+z+100 is a
Solution:
QUESTION: 5

The expression 7xy has the factors
Solution: The expression has different factors that are 7,x,y because an expression can't be made without factors.
QUESTION: 6

The common factors of 2y. 22xy is
Solution:

Factors of 22xy are 2*11*x*y, so common factors are 2y.

QUESTION: 7

‘2’ is common factor of the expressions
Solution:
QUESTION: 8

The factorization of 7a2+14a is
Solution:
QUESTION: 9

The addition of ab-bc, bc-ca, ca-ab is
Solution:

ab-bc+bc-ca+ca-ab=0, because we have ab-ab,bc-bc,ca-ca all equal to zero.

QUESTION: 10

One of the example of binomial is
Solution:
QUESTION: 11

The area of rectangle is’ xy’ where’ x’ is length and ‘y’ is breadth. If the length of rectangle is increased by 5 units and breadth is decreased by 3 units, the new area of rectangle will be
Solution:

initial area = xy

after increaasing length by 5 units and breadth is decreased by 3 units

new length = x+5

new breadth = y-3

new area = (x+5)(y-3)

QUESTION: 12

The value of 2x (-3x) is
Solution: We must multiply 2 with 3 an we get -6 and multiply x with x is equal to x2 therefore d is the answer.
QUESTION: 13

Like terms in the expression 7x,5x2,7y, -5yx, -9x2, are
Solution:

Like terms consist of same variables with same powers.

QUESTION: 14

Area of rectangle of length’ 3x’ and breadth ‘5y ‘is
Solution:
QUESTION: 15

Number of terms in the expression xyz+1 is
Solution:
QUESTION: 16

The product of -4p and 7p is
Solution:
QUESTION: 17

What degree does x3 - x2y2 - 8y2+ 2 have?
Solution:

The correct answer is c

   The given quadratic polynomial:

To find the highest degree of the polynomial 

The degree of  = 3

The degree of  = 2 + 2 = 4

The degree of  = 2 and

The degree of 2 = 0

∴ The highest degree of the given polynomial = 4

Hence, the highest degree of the given polynomial = 4

QUESTION: 18

Multiplication of pq+qr+rp and ‘zero’ is
Solution:
QUESTION: 19

The value of 3x(4x-5)+3 for x = 3
Solution:
QUESTION: 20

The volume of rectangular box whose length, breadth and height is 2p,4q.8r respectively is
Solution:

length = 2p
breadth =4q
height =8r
Volume = length x breadth x height
=2p x 4q x 8r
=64pqr
Answer : 64pqr

QUESTION: 21

Numerical coefficient of x2y in the expression 1+x+2x2y is
Solution:
QUESTION: 22

What is the value of 5x25 - 3x32 + 2x-12 at x = 1 ?
Solution:

The correct answer is c

5x^25-3x^32+2x^-12

By putting value of x = 1

5(1)^25 - 3(1)^32 + 2(1)^-12

5×(1) - 3×(1) + 2×(1)

If we give 1 any raised power the answer is always 1 .e.g 1^4= 1×1×1×1=1

=5 - 3 + 2.

= 2 + 2.

= 4

 

 

QUESTION: 23

Which of the following expression is trinomial
Solution:
QUESTION: 24

Which of the following expression is monomial
Solution:
QUESTION: 25

Multiplication of ‘ab’ and ‘a-b’ is
Solution:
QUESTION: 26

The suitable identity to find (x+3)(x+3) is
Solution:
QUESTION: 27

Value of (4p – 3q)2 is
Solution:

Using (a - b)2 
(4p - 3q)2 
= 16p2 - 24pq + 9q2

QUESTION: 28

(9x+a)(x+b) is equal to
Solution:

9x(x+b)+a(x+b)

=9x2 + 9bx+ax+ab

=9x2+x(9b+a)+ab

QUESTION: 29

Value of expression ‘a(a2+a +1)+5’ for ‘ a’ = 0 is
Solution: It's correct ans would be 5 because if a,=0 then a( a²+ a+ 1)+5 so, if a=0 then, 0(0²+ 0+ 1) +5 0x(0x0+0+1)+5 0x1 +5 any no multiplied by 0 is 0 so, 0x1 =0+5=5 therefore, the correct ans is 5.
QUESTION: 30

Which of the following is not binomial
Solution:
QUESTION: 31

Subtracting 7x +y from –x +y gives
Solution:

-x + y - (7x + y)

= -8x

QUESTION: 32

Which identity is used to evaluate (m+3)(m+2).
Solution:
QUESTION: 33

Use suitable identity to evaluate 992.
Solution:

99 can be written as 100-1

992 = (100 -1)2 = 1002 + 1 -200

= 10000 + 1 -200

= 9801

 

QUESTION: 34

Evaluate (4x+y)2 by suitable identity
Solution:
QUESTION: 35

Find the value of 95 x 102 by suitable identity.
Solution:

95 x 102 = (100-5)(100+2) = 1002+(-5+2)100+(-5)2 = 10000-300-10 = 9690

QUESTION: 36

Which of the following is obtained by subtracting x2-y2 from y2 - x2?
Solution:

y2 - x2 - ( x2 - y2)

= 2y2 - 2x2

= -2(x2  - y2)

QUESTION: 37

(a-b)2 is equal to
Solution:
QUESTION: 38

Using identity a2 – b2 = (a+b)(a-b), find 42-62
Solution:

42 - 62=(4-6)(4+6)=-2*10=-20

QUESTION: 39

The expression in one variable is
Solution:

Since option (b),(c) and (d) have two variables x and y ,the answer is x+x2+1

QUESTION: 40

(a+b)(a-b) is equal to
Solution:
Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us