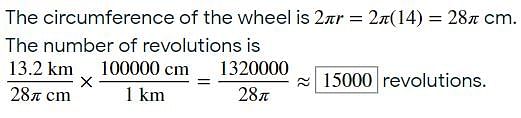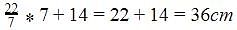Test: Area & Perimeter of A Circle - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - Test: Area & Perimeter of A Circle
A wire is bent in the form of a circle of radius 28 cm. It is bent to form a square. The length of the side of the square will be
The radius of a circle if its perimeter and area are numerically equal is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The diameter of a cycle wheel is 28 cm. The number of revolutions it makes in moving 13.2 km is
Find the circumference of the circle, whose area is 144π cm2
The area of a circular pizza is 616 cm2. Its diameter is
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 40 cm and 9 cm is:
The area of a circle with diameter 6 m exceeds the combined areas of circles with diameters 4m and 2 m by
The area of a circular plot is 9856 sq. m. The cost of fencing the plot at the rate of Rs. 6 per meter will be
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
If the circumference of a circle increases from 2 to 4 then its area is
A sector of a circle of radius 10.5 cm subtends an angle of 45° at the centre of the circle as in adjoining figure. Find the perimeter of sector.
If the side of an equilateral triangle and the radius of a circle are equal, find the ratio of their areas.
The radii of two circles are 19 cm and 9 cm respectively. The radius of the circle which has its circumference equal to the sum of the circumferences of the two circles is:
The sum of the diameters of two circles is 280 cm and the difference of their circumferences is 88 cm. Then the larger of the two radii is
If the perimeter and area of a circle are numerically equal, then the radius of the circle is
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
If the difference between the circumference and the radius of a circle is 37 cm, then using π = 22/7, the circumference (in cm) of the circle is:
The length of the line that marks out a circle and its region is the
If C is the circumference of a circle of radius r, then perimeter of one of the quadrants will be
If the diameter of semicircular protractor is 14 cm, then its perimeter is:
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is
If the perimeter of a sector of a circle of radius 5.2 cm. is 16.4 cm. What multiple of the radius is the area of the sector?
A garden roller has a circumference of 4 m. The number of revolutions it makes in moving 40 metres are:
The shaded part of the circle in the given figure represents a
The ratio of radii of two circles is in the ratio of 1:5. Calculate the ratio of their perimeters.
|
123 videos|457 docs|77 tests
|
|
123 videos|457 docs|77 tests
|