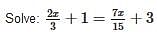Test: Linear Equations- 2 - Class 8 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 8 - Test: Linear Equations- 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The sum of three consecutive multiples of 7 is 357. Find the smallest multiple.
In an equation the values of the expressions on the LHS and RHS are _______.
The sum of two digit number and the number formed by interchanging its digit is 110. If ten is subtracted from the first number, the new number is 4 more than 5 times of the sum of the digits in the first number. Find the first number.
What will be the solution of these equations ax+by = a-b, bx-ay = a+b
The present age of Sahil’s mother is three times the present age of Sahil. After 5 years their ages will add to 66 years. Find their present ages.
Amina thinks of a number and subtracts 5/2 from it. She multiplies the result by 8. The result now obtained is 3 times the same number she thought of. What is the number?
Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
The value of the expression on one side of the equality sign is _____ to the value of the expression on the other side.
Arjun is twice as old as Shriya. Five years ago his age was three times Shriya’s age. Find their present ages.
8 men and 12 boys can finish a piece of work in 10 days while 6 men and 8 boys can finish the work in 14 days. find the time taking by 1 man alone and 1 boy alone to finish the same work.
|
79 videos|408 docs|31 tests
|
|
79 videos|408 docs|31 tests
|