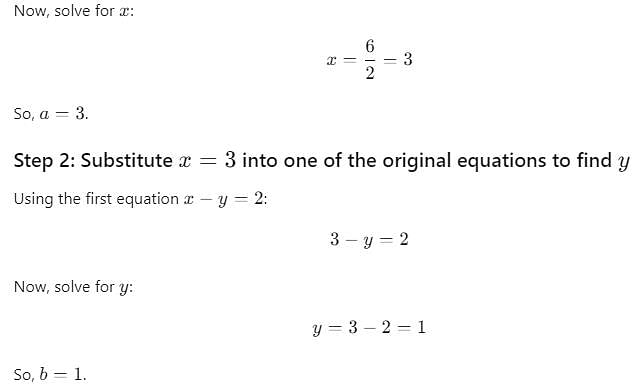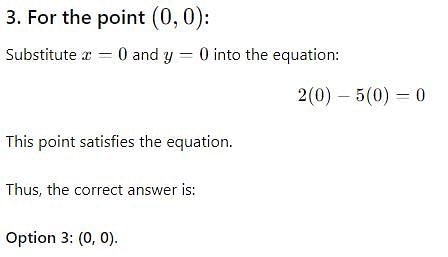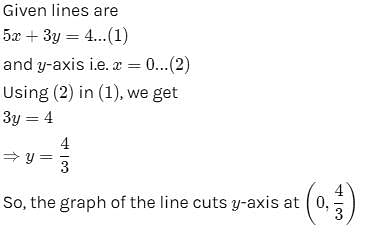Test: Linear Equations In Two Variables - 1 - Class 9 MCQ
23 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Linear Equations In Two Variables - 1
The graph of the linear equation 2x – 3y = 6, cuts the y-axis at the point
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Solve x + 4y = 14 .....(i)
7x - 3y = 5 ....(ii)
A linear equation in two variables has maximum :
The solution of the equation x + y = 3, 3x – 2y = 4 is :
x = 2, y = – 1 is a solution of the line equal to :
The value of x satisfying the equation x2 + p2 = (q – x)2 is :
If x = a, y = b is the solution of the pair of equation x-y = 2 and x+y = 4 then what will be value of a and b
The point of the form (2a, -a) lies on
The sum of a two digit number and the number obtained by reversing the order of the digits is 187. If the digits differ by 1, then what will be the number?
The straight line 2x – 5y = 0 passes through the point :
If x = 1,y = 1 is a solution of equation 9ax + 12ay = 63 then, the value of a is :
The point of the form (a, -a), where a ≠ 0, lies on
The straight line passing through the points (0, 0), (–1, 1) and (1, – 1) has the equation :
Which of the following equations is not linear equation :
The graph of the linear equation 3x – 2y = 6, cuts the x-axis at the point
The sum of two digits and the number formed by interchanging its digit is 110. If ten is subtracted from the first number, the new number is 4 more than 5 times of the sum of the digits in the first number. Find the first number.
The graph of the equation y = x2 is :
The graph of the lines x + y = 7 and x – y = 3 meet at the point :
The graph of the equation 2x – 3 = 3x – 5 is parallel to :
The graph of the line 5x + 3y = 4 cuts y-axis at the point :
|
44 videos|412 docs|55 tests
|
|
44 videos|412 docs|55 tests
|


 \
\