Get the App Signup / Login
Sign in Open App

Test: Lines And Angles- 2


25 Questions MCQ Test NCERT Mathematics for CAT Preparation | Test: Lines And Angles- 2


Description
Attempt Test: Lines And Angles- 2 | 25 questions in 25 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study NCERT Mathematics for CAT Preparation for Class 9 Exam | Download free PDF with solutions
QUESTION: 1

An exterior angle of a triangle is 80°and two interior opposite angles are equal. Measure of each of these angles is :

Solution:

Exterior angle = sum of two interior opposite angle so, exterior angle =1/2×80 = 40°

 

QUESTION: 2

An exterior angle of a triangle is 800 and the interior opposite angles are in the ratio 1 : 3. Measure of each interior opposite angle is :

Solution: X+3x=80(exterior angle of triangle is equal to two interior opposite angles) 4x=80 x=80/4 x=20 So, x=20 and 3x=3*20=60 are two opposite interior angles.
QUESTION: 3

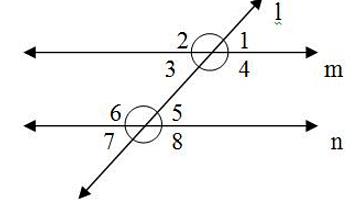
In the adjoining figure, if m ║ n, then ∠4 + ∠7 is equal to –


 

 

Solution:
QUESTION: 4

If two angles are supplementary and the larger is 200 less then three times the smaller, then the angles are :-
Solution:
supplementary = 180 degrees
larger = 3x - 20
smaller = x 
3x - 20 + x = 180
4x - 20 = 180

4x = 180 + 20
4x = 200
4x/4 = 200/4
x = 50 
smaller = 50 degrees
larger = 3(50) - 20 = 150 - 20 = 130 degrees
QUESTION: 5

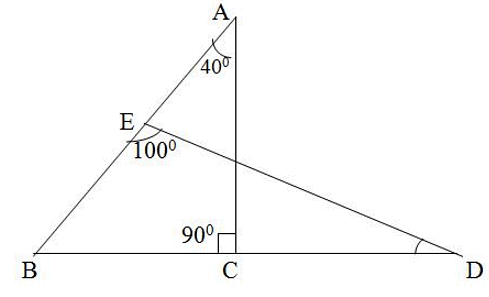
In the given figure, ∠BAC = 400, ∠ACB = 900 and ∠BED = 1000, Then ∠BDE = ?
Solution:
QUESTION: 6

The angle which is equal to 8 times its complement is :
Solution:
QUESTION: 7

Two planes intersect each other to form a :
Solution: Two non-parallel planes in space form a line upon intersection, as long as each plane is unique. Three non-parallel planes intersect at a point. The best and simplest example is to fold a piece of paper. Since the folded paper now represents two distinct planes, the crease itself is the intersection point, forming a line.
QUESTION: 8

In the adjoining figure, m ║ n, if ∠1 = 500, then ∠2 is equal to –

 
Solution:
QUESTION: 9

In a right-angled triangle where angle A = 90° and AB = AC. What are the values of angle B?
Solution:

∵ In ∆ABC,
AB = AC
∴ ∠B = ∠C    ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆ABC,
∠A + ∠B + ∠C = 180°
| Sum of all the angles of a triangle is 180°
⇒ 90° + ∠B + ∠C = 180°
| ∵ ∠A = 90° (given)
⇒    ∠B + ∠C = 90°    ...(2)
From (1) and (2), we get
∠B = ∠C = 45°.

QUESTION: 10

In the given figure, BO and CO are the bisectors of ∠B and ∠C respectively. If ∠A = 500, then ∠BOC = ?
Solution:

a+b+c = 180
50+b+c= 180
b+c = 130 ............(1)
divide equation (1) by 2 
1/2(b+c) = 65...........(2)
now in triangle obc
o+1/2(b+c) = 180
o+65= 180 ( from (2))
o= 180-65= 115 

QUESTION: 11

An exterior angle of a triangle is 800 and the interior opposite angles are in the ratio 1 : 3. Measure of each inte4rior opposite angle is :
Solution:

Let the interior angles be x and 3x 

We know that exterior angle of triangle is equal to sum of interior opposite angles.

⇒ x+3x=80∘

⇒ 4x=80∘

⇒ x=20∘

So the angles are 

x=20∘

3x=3×20∘

= 60∘

QUESTION: 12

In figure, AB and CD are parallel to each other. The value of x is :
Solution:
QUESTION: 13

In the adjoining figure, m ║ n. If ∠a : ∠b = 2 : 3, then the measure of ∠h is –
Solution:

A+b =180(linear pair)

2x+3x=180

5x=180

x=180/5

x=36

a=2x=2*36=72

b=3x=3*36=108

b=d (vertical opposite angles are equal)

d=f (alternative interior angles are equal)

f=h (vertically opposite angles are equal)

So, h= 108

QUESTION: 14

In the given figure, the measure of ∠ABC is :
Solution:
QUESTION: 15

In the given figure, AB ∥ CD. If ∠EAB = 500 and ∠ECD = 600, then ∠AEB = ?
Solution:
QUESTION: 16

In the given figure, the value of x which makes POQ a straight line is :
Solution: 2x+ 30+ 4x = 180 6x = 150 x = 25
QUESTION: 17

In two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 5 : 4, then the smaller of the two angles is :
Solution:
QUESTION: 18

In the adjoining figure, AB ║ CD and AB ║ EF. The value of x is :-
Solution:

Given, AB ║ CD and AB ║ EF

so CD || EF

which means ∠ECD + ∠CEF = 1800 (corresponding angles)

∠ECD = 180 - 150 = 300

since AB || CD so 

∠ABC= ∠BCD (alternate interior angles)

∠ABC = 30 + ∠ECD = 30 + 30 = 600

QUESTION: 19

In the adjoining figure, the bisectors of ∠CBD and ∠BCE meet at the point O. If ∠BAC = 700, then ∠BOC is equal to :-

 
Solution:
QUESTION: 20

In the given figure, ∠OEB = 750, ∠OBE = 550 and ∠OCD = 1000. Then ∠ODC = ?
Solution:
QUESTION: 21

If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3, then the largest of two angles is :
Solution:
QUESTION: 22

Sum of all angles around a main point equals to
Solution:
QUESTION: 23

What is the supplement of 105°      
Solution:
QUESTION: 24

In the adjoining figure, BE and CE are bisectors of ∠ABC and ∠ACD respectively. If ∠BEC = 250, then ∠BAC is equal to :-
Solution:
QUESTION: 25

Find the angle if six times of its complement 12° less than twice of its supplement?
Solution:
Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us