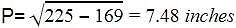Test: Problems on Pythagoras Theorem
10 Questions MCQ Test NCERT Mathematics for CAT Preparation | Test: Problems on Pythagoras Theorem
The monitors of computers are measured along the diagonal. What is the size of the largest monitor that can be placed in a space measuring 17″ x 21″?
Since monitors are measured along the diagonals this means we need to use pythagoras theorem for this right angled triangle.
H2 = P2 + B2
=17 * 17 + 21 * 21
=289 + 441 = 730
H=27’’ (Approx)
If the legs of an isosceles right triangle are 5 cm long, approximate the length of the hypotenuse to the nearest whole number.
Find the height of the given triangle if its base is 26 inches and the slant side is 15 inches long as shown below.
Height of the triangle is the altitude. SInce the triangle is an isosceles triangle its median is equal to its altitude . So this means that the altitude is perpendicular and bisects the opposite side .
So BD=DC=26/2=13
So in right angled Triangle,
Using Pythagoras theorem,
H2 = P2 + B2
225 = P2 + 169
If the sum of the squares of a and b is the same as the square of c and if m < n, then for what value of k can the Pythagorean triples be generated with the following equations?
a = n2 + k , b = 2mn : c = m2 + n2
Find the total perimeter of the given figure.
What is the diagonal length of a TV screen whose dimensions are 80 cm x 60 cm?
If the sum of the length of the legs of a right triangle is 49 cm and the hypotenuse is 41 cm, find its shortest side.
Sum of the length of the legs of a right angle triangle is 49
So let one leg be x, other will be 49-x
Applying Pythagoras theorem,
H2=P2+B2
41*41=x2+(49-x)2
1681=x2 + 2401 + x2 - 98x
2x2- 98x + 720 = 0
Dividing the equation by 2
x2 - 49x + 360 = 0
x2 - 9x - 40x + 360 = 0
x (x - 9) - 40 (x - 9) = 0
(x - 9)(x - 40) = 0
So x is either 9 or 40,
So the smaller side is 9 cm
How far up a wall will an 11m ladder reach, if the foot of the ladder is 4m away from the wall?
The height of wall will be the perpendicular for the right angle triangle. So applying pythagoras theorem
H2=P2+B2
11*11=P2+16
P=121-16=10.2 cm
A wood frame for pouring concrete has an interior perimeter of 14 metres. Its length is one metre greater than its width. The frame is to be braced with twelve-gauge steel cross-wires. Assuming an extra half-metre of wire is used at either end of a cross-wire for anchoring, what length of wire should be cut for each brace?
Let width is x
Then length is x+1
Perimeter =x +x + x + 1 + x + 1 = 14
4 x= 12
x = 3
length = 4
Using Pythagoras theorem,
H2 = P2 + B2
=9 + 16 = 25
H = 5cm
An extra half meter on either side will give the length of the wire as 5 + 1 = 6cm
Anuj swims across a pool diagonally every day. The pool is 4 m wide, and it is 16 m diagonally across. What is the length of the pool?
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Download free EduRev App
Related tests
|
|
|
|
|
|
© EduRev
|
Follow Us
|