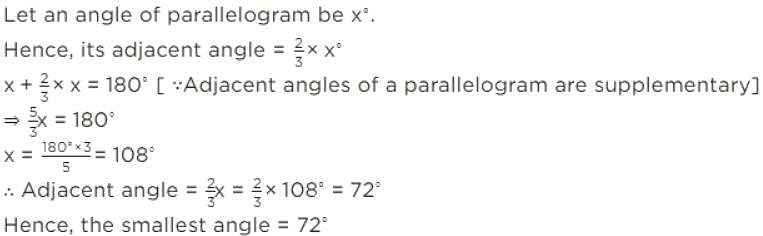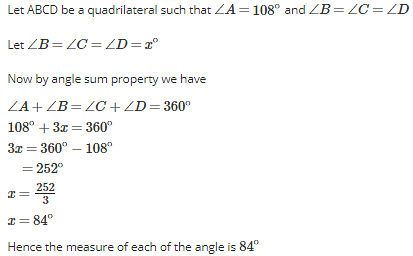Test: Quadrilaterals- 1 - Class 9 MCQ
25 Questions MCQ Test Online MCQ Tests for Class 9 - Test: Quadrilaterals- 1
The length of each side of a rhombus is 10cm and one of its diagonal is of length 16cm. The Length of the other Diagonal is:
In a Quadrilateral ABCD, AB = BC and CD = DA, then the quadrilateral is a
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
ABCD is a Parallelogram in which AB = 9.5cm and its perimeter is 30cm. Find the length of each side of the Parallelogram?
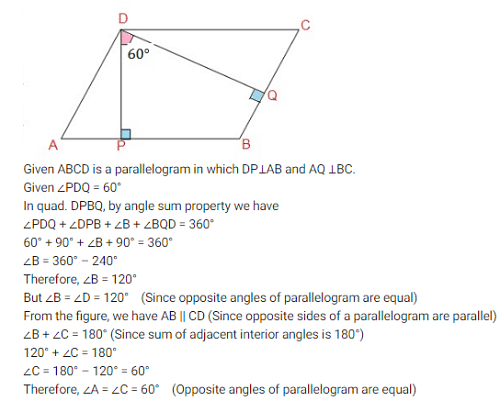
The angle between two altitudes of a Parallelogram through the vertex of an obtuse angle of the Parallelogram of 60∘. Find the angles of the Parallelogram
If an angle of a parallelogram is two-third of its adjacent angle, then find the smallest angle of the parallelogram.
If ABCD is a Parallelogram with 2 Adjacent angles ∠A =∠B, then the parallelogram is a
Given a triangular prism, then what can we conclude about the lateral faces?
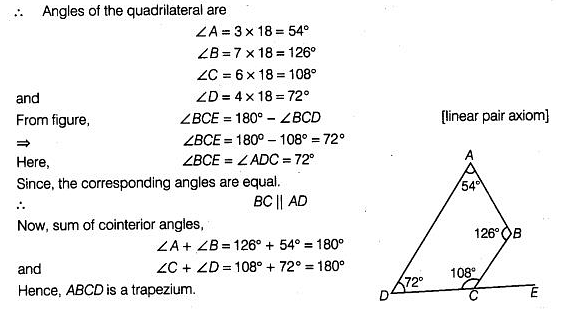
If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3:7:6:4, then ABCD is
ABCD is a Trapezium in which AB∥DC and ∠A = ∠B = 45∘. Find angles C and D of the Trapezium
Angles of a quadrilateral are in the ratio 3 : 6 : 8: 13. The largest angle is :
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is:
The angles of a quadrilateral are in the ratio 4: 5: 10: 11. The angles are
One Angle of a quadrilateral is of 108∘ and the remaining three angles are equal. Find each of the three equal angles.
ABCD is a Rectangle. Find the values of x and y?

AB =30 DA= 14 DC= x+y CB=x-y
If area of a Parallelogram with sides ‘a’ and ‘b’ is A and that of a rectangle with sides ‘a’ and ‘b’ is B, then
A diagonal of a Rectangle is inclines to one side of the rectangle at an angle of 25∘. The Acute Angle between the diagonals is :
Diagonals of a Parallelogram ABCD intersect at O. If ∠BOC = 90∘, ∠BDC = 50∘ then ∠OAB is
Angles of a quadrilateral are in the ratio 3 : 4 : 4 : 7. Find all the angles of the quadrilateral.
In Triangle ABC which is right angled at B. Given that AB = 9cm, AC = 15cm and D, E are the mid-points of the sides AB and AC res. Find the length of BC?
The Parallel sides of a trapezium are ‘a’ and ‘b’ res. The line joining the mid-points of its non-parallel sides will be
If a diagonal AC and BD of a quadrilateral ABCD bisect each other, then ABCD is a
Which of the following is not true for the Parallelogram?
The angles of the quadrilateral are in the ratios 3 : 5 : 9 : 13. Find all the angles of the Quadrilateral
The length of each side of a rhombus is 10cm and one of its diagonal is of length 16cm. The Length of the other Diagonal is:
|
5 docs|314 tests
|