Class 7 Exam > Class 7 Tests > Mathematics (Maths) Class 7 > Test: The Triangle and Its Properties - Class 7 MCQ
Test: The Triangle and Its Properties - Class 7 MCQ
Test Description
15 Questions MCQ Test Mathematics (Maths) Class 7 - Test: The Triangle and Its Properties
Test: The Triangle and Its Properties for Class 7 2024 is part of Mathematics (Maths) Class 7 preparation. The Test: The Triangle and Its Properties questions and answers have been
prepared according to the Class 7 exam syllabus.The Test: The Triangle and Its Properties MCQs are made for Class 7 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: The Triangle and Its Properties below.
Solutions of Test: The Triangle and Its Properties questions in English are available as part of our Mathematics (Maths) Class 7 for Class 7 & Test: The Triangle and Its Properties solutions in
Hindi for Mathematics (Maths) Class 7 course. Download more important topics, notes, lectures and mock
test series for Class 7 Exam by signing up for free. Attempt Test: The Triangle and Its Properties | 15 questions in 10 minutes | Mock test for Class 7 preparation | Free important questions MCQ to study Mathematics (Maths) Class 7 for Class 7 Exam | Download free PDF with solutions
Detailed Solution for Test: The Triangle and Its Properties - Question 1
Test: The Triangle and Its Properties - Question 2
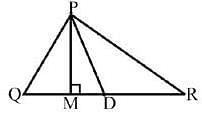
A/an _____________ connect a vertex of a triangle to the mid-point of the opposite side.
Detailed Solution for Test: The Triangle and Its Properties - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for Test: The Triangle and Its Properties - Question 3
Test: The Triangle and Its Properties - Question 4
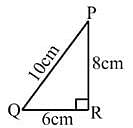
ΔABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.
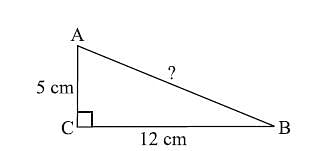
Detailed Solution for Test: The Triangle and Its Properties - Question 4
Detailed Solution for Test: The Triangle and Its Properties - Question 5
Detailed Solution for Test: The Triangle and Its Properties - Question 6
Detailed Solution for Test: The Triangle and Its Properties - Question 7
Test: The Triangle and Its Properties - Question 8
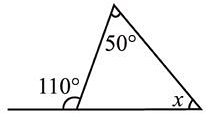
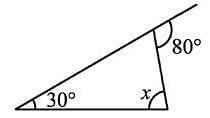
Find the value of x in the adjoining figure.
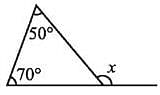
Detailed Solution for Test: The Triangle and Its Properties - Question 8
Detailed Solution for Test: The Triangle and Its Properties - Question 9
Detailed Solution for Test: The Triangle and Its Properties - Question 10
Test: The Triangle and Its Properties - Question 11
If the angles of a triangle are in the ratio 4:5:9. Find all the angles of a the triangle
Detailed Solution for Test: The Triangle and Its Properties - Question 11
Test: The Triangle and Its Properties - Question 12
The triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a
Detailed Solution for Test: The Triangle and Its Properties - Question 12
Test: The Triangle and Its Properties - Question 13
One of the angles of a triangle is 110° and the other two angles are equal what is the measure of each of these equal angles
Detailed Solution for Test: The Triangle and Its Properties - Question 13
Test: The Triangle and Its Properties - Question 14
The measure of three angles of a triangle are in the ratio 5:3:1.find the measure of this angles
Detailed Solution for Test: The Triangle and Its Properties - Question 14
Test: The Triangle and Its Properties - Question 15
The altitude and median be same for a which triangle?
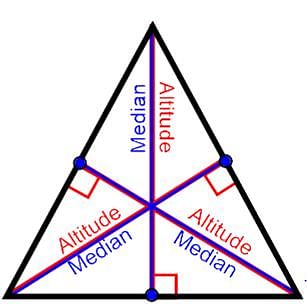
Detailed Solution for Test: The Triangle and Its Properties - Question 15
|
76 videos|345 docs|39 tests
|
Information about Test: The Triangle and Its Properties Page
In this test you can find the Exam questions for Test: The Triangle and Its Properties solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: The Triangle and Its Properties, EduRev gives you an ample number of Online tests for practice
|
76 videos|345 docs|39 tests
|
Download as PDF