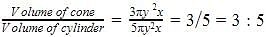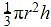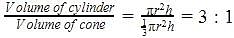Test: Volume Combination of Solids - Class 10 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 10 - Test: Volume Combination of Solids
The radius of a cylindrical tank is 28m. If its capacity is equal to that of a rectangular tank of size 28mx16mx11m, then its depth is
The ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cone and a cylinder have their heights in the ratio 4: 5 and their diameters are in the ratio 3: 2. The ratio of their volumes will be
A container is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is 24 cm and the total height of the container is 16 cm. Its capacity is
The volume of a sphere (in cu. cm) is equal to its surface area (in sq. cm). The diameter of the sphere (in cm) is
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm and the heights of the cylindrical and conical portions are 12 cm and 7 cm respectively. The approximate volume of the toy will be
A cylinder, a cone and a hemisphere are of equal base and have the same height. The ratio of their volumes is
A spherical steel ball is melted to make 8 new identical balls. Then the radius of each new ball is how much times the radius of the original ball
A river 3 m deep and 10 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
A largest sphere is carved out of a cube of side 7cm. The volume of the sphere is
A cylinder whose height is two thirds of its diameter has the same volume as a sphere of radius 4 cm. The radius of the base of the cylinder will be
The radii of two right circular cylinders are in the ratio 2: 3 and their heights are in the ratio 5: 4. The ratio of their volumes will be
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the a hemisphere is 3.5 cm and height of cone outside the hemisphere is 5 cm, find the volume of the water left in the tub.
The surface area of a cube is equal to the surface area of a sphere. The ratio of their volumes will be
The volume of a largest sphere than can be cut from cylindrical log of wood of base radius 1 m and height 4 m is:
A cylindrical vessel of diameter 42 cm and height 40 cm contains water up to a depth of 16 cm. Now a solid iron cylinder, with diameter 14 cm and height 32 cm is placed upright in the cylindrical vessel. The volume of the water required to just submerge the solid cylinder will be
A rectangular paper is 44 cm long and 20 cm wide. A cylinder is formed by rolling the paper along its length. The volume of the cylinder will be
A cylinder, a cone and a hemisphere have equal base and height. Find the ratio of their volumes
A cylinder and a cone are of same base radius and of same height. The ratio of the volume of cylinder to that of the cone is:
|
123 videos|457 docs|77 tests
|
|
123 videos|457 docs|77 tests
|


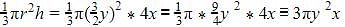 Volume of cylinder= πr2h=y2*5x
Volume of cylinder= πr2h=y2*5x