Test: Kinematics and Dynamics of Rotational Motion about a Fixed Axis (July 27) - NEET MCQ
10 Questions MCQ Test Daily Test for NEET Preparation - Test: Kinematics and Dynamics of Rotational Motion about a Fixed Axis (July 27)
Kinetic energy of a rolling object is the
If we apply Newton’s First Law to torque then the statement will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A torque of 20 Nm is applied to a flywheel of mass 10 kg and radius of gyration 50 cm. The resulting angular acceleration is:
A rigid body is rotating about an axis. Different particles are at different distances from the axis. Which of the following is true?
A ball is under the effect of circular motion about a perpendicular axis with respect to the reference direction. The angular position (in radians) is given by the following function θ = t2 - 0.4t + 2 .The angular position when angular velocity is zero is
The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 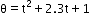 . The linear velocity of the particle
. The linear velocity of the particle
Which of the following is not a unit of angular displacement?
A boy is playing with a tire of radius 0.5m. He accelerates it from 5rpm to 25 rpm in 15 seconds. The linear acceleration of tire is
A demo CD, 8 cm in diameter, spins 200 rev/min. Determine its linear velocity in cm/s for a point 3 cm from the center.
A wheel rotates with a constant acceleration of 2.0 rad/s2 . If the wheel starts from rest, the number of revolutions it makes in the first ten seconds will be approximately:
|
12 docs|366 tests
|

















