RS Aggarwal Test: Real Numbers - 3 - Class 10 MCQ
25 Questions MCQ Test Online MCQ Tests for Class 10 - RS Aggarwal Test: Real Numbers - 3
Pairs of natural numbers whose least common multiple is 78 and the greatest common divisor is 13 are:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If two positive integers p and q are written as p=a2b2 and q=a3b, a,b are prime numbers then verify that L.C.M.(p,q)×H.C.F.(p,q)=pq
Two natural numbers whose sum is 85 and the least common multiple is 102 are:
If p is a positive prime integer, then √p is –
If a is a positive integer and p be a prime number and p divides a2, then
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
If x = and y =
, then the value of (x2 + y2) is
If two positive integers a and b are written as a = x3y2 and b = xy3; x, y are prime numbers, then HCF (a, b) is
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
Three pieces of timber 42 m, 49 m and 63 m long have to be divided into planks of the same length. What is the greatest possible length of each plank? How many planks are formed?
|
461 tests
|


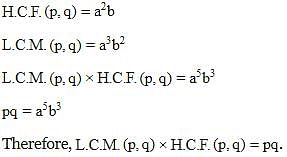
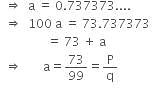

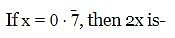
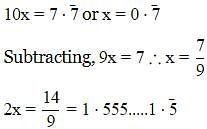

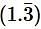 is equal to –
is equal to –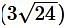 is -
is -

















