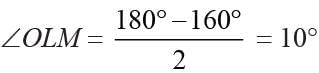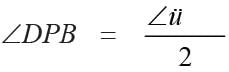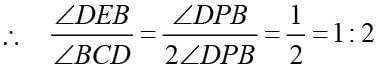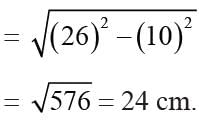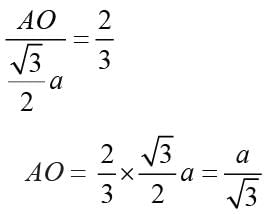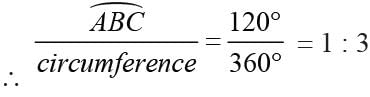Math Olympiad Test: Circles- 2 - Class 9 MCQ
15 Questions MCQ Test - Math Olympiad Test: Circles- 2
In the adjoining figure, O is the circumcentre of ∆ABC, then the value of ∠OBC + ∠BAC is

In the adjoining figure, AB = AC, and ∠ACB = 64°, then ∠BEC =?
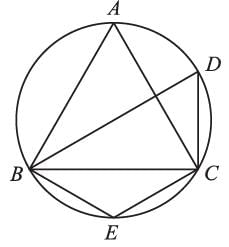

AB || CD, and ∠B = 65° and ∠DAC = 30° The measure of ∠CAB =?
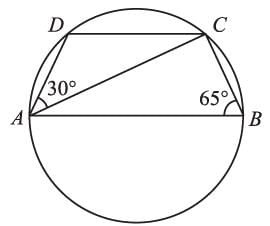

The measures of AB and CD are equal, and the measure of ∠LOM = 160°. The measure of ∠OLM is:
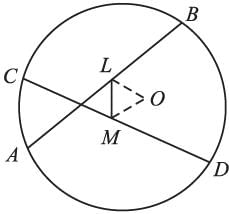
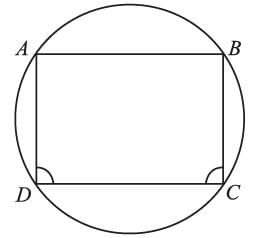
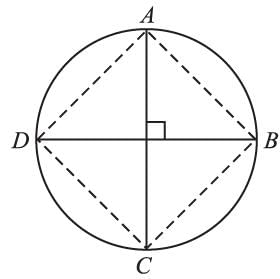
If the two diameters of a circle intersect at 90°. The figure formed by joining the endpoint of the diameters will be a:
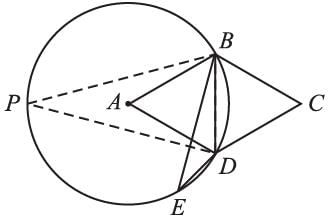
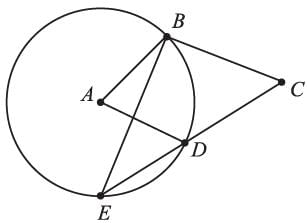
A is the center of the circle. ABCD is a parallelogram and CDE is a straight line. the ratio ∠DEB : ∠BCD is
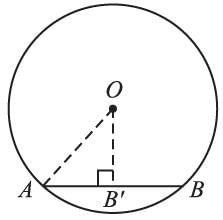
The radius of a circle is 26 cm and the length of the perpendicular from the center to the chord AB is equal to 10 cm. The length of AB is:
The radius of the circumcircle of an equilateral triangle having a length of each side equal to ‘a’ is:
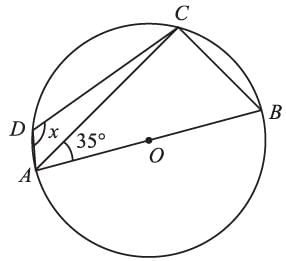
AB and AC are two equal chords of a circle whose center is O. If AB ⊥ OD and OE ⊥ AC, then,
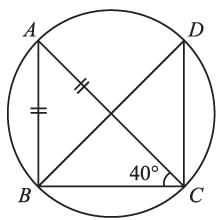
In the adjoining figure, AB = AC and ∠ACB = 40°, then ∠BDC =?
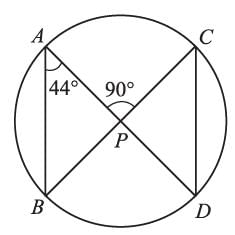
Chords AD and BC intersect each other at right angles at point P. If ∠DAB = 44°, then ∠ADC =?
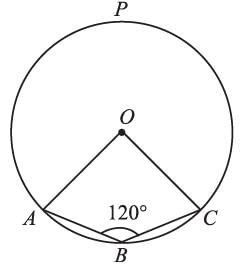
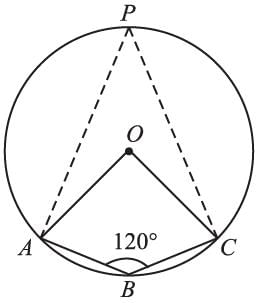
If the length of an arc of a circle is proportional to the angle subtended by it at the center. Then, the ratio of ABC : circumference =?