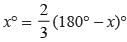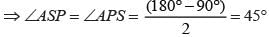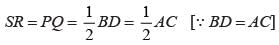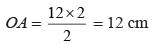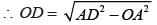Math Olympiad Test: Quadrilaterals- 2 - Class 9 MCQ
15 Questions MCQ Test - Math Olympiad Test: Quadrilaterals- 2
In a quadrilateral, the angles are in the ratio 1 : 2 : 3 : 4. What is the value of largest angle?
The perimeter of a parallelogram is 24 cm. If the longer side measures 8 cm. Then what is the measure of the shorter side?
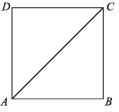
ABCD is a square. What is the value of ∠ACD?

The figure formed by joining the mid-points of consecutive sides of a quadrilateral is a
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. What is the difference between largest and smallest angle?
If an angle of a parallelogram is two third of its adjacent angle what is the measure of smallest angle of parallelogram?
If ∠P, ∠Q, ∠R, ∠S of a quadrilateral PQRS, taken in order are in the ratio 3 : 7 : 6 : 4, then PQRS is a
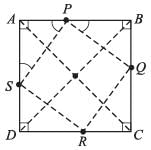
The figure formed by joining the mid-points of the adjacent sides of a square is
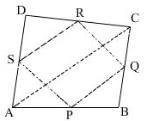
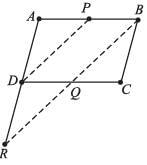
D is the mid-point of side AB of a parallelogram ABCD. A line through B parallel to PD meets DC at Q and AD produced at R, then which of the following is correct?
If ABCD is a square then what is the measure of ∠DCA?
Two opposite angles of a parallelogram are (3x - 2)° and (50 - x)°. Find the smallest angle.
If an angle of a parallelogram is one third of its adjacent angle then what is the measure of smallest angle?
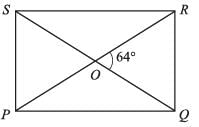
The diagonals of a rectangle PQRS meet at O. If ∠ROQ = 64° then Find ∠PSO?
The angles of a quadrilateral are 98°, 92°, 70° respectively. What is the measure of 4th angle?
If the length of each side of rhombus is 15 cm and one of its diagonals is 24 cm what is length of other diagonal?