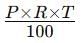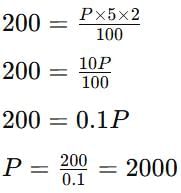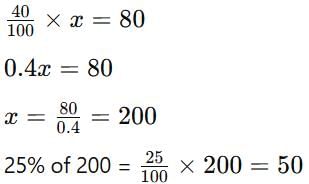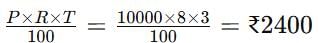Class 7 Exam > Class 7 Tests > Mathematics (Maths) Class 7 > Important Questions: Comparing Quantities - Class 7 MCQ
Important Questions: Comparing Quantities - Class 7 MCQ
Test Description
10 Questions MCQ Test Mathematics (Maths) Class 7 - Important Questions: Comparing Quantities
Important Questions: Comparing Quantities for Class 7 2024 is part of Mathematics (Maths) Class 7 preparation. The Important Questions: Comparing Quantities questions and answers have been
prepared according to the Class 7 exam syllabus.The Important Questions: Comparing Quantities MCQs are made for Class 7 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Important Questions: Comparing Quantities below.
Solutions of Important Questions: Comparing Quantities questions in English are available as part of our Mathematics (Maths) Class 7 for Class 7 & Important Questions: Comparing Quantities solutions in
Hindi for Mathematics (Maths) Class 7 course. Download more important topics, notes, lectures and mock
test series for Class 7 Exam by signing up for free. Attempt Important Questions: Comparing Quantities | 10 questions in 20 minutes | Mock test for Class 7 preparation | Free important questions MCQ to study Mathematics (Maths) Class 7 for Class 7 Exam | Download free PDF with solutions
Important Questions: Comparing Quantities - Question 1
What is the meaning of the term 'percentage'?
Detailed Solution for Important Questions: Comparing Quantities - Question 1
Important Questions: Comparing Quantities - Question 2
If 30% of a number is 90, what is the original number?
Detailed Solution for Important Questions: Comparing Quantities - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Important Questions: Comparing Quantities - Question 3
Convert the fraction 3/4 to a percentage.
Detailed Solution for Important Questions: Comparing Quantities - Question 3
Important Questions: Comparing Quantities - Question 4
A shopkeeper buys an item for ₹500 and sells it for ₹600. What is the profit percentage?
Detailed Solution for Important Questions: Comparing Quantities - Question 4
Important Questions: Comparing Quantities - Question 5
If the simple interest on a sum of money for 2 years at 5% per annum is ₹200, what is the principal amount?
Detailed Solution for Important Questions: Comparing Quantities - Question 5
Important Questions: Comparing Quantities - Question 6
What is the percentage increase if a quantity rises from 50 to 75?
Detailed Solution for Important Questions: Comparing Quantities - Question 6
Important Questions: Comparing Quantities - Question 7
If 40% of a number is 80, what is 25% of the same number?
Detailed Solution for Important Questions: Comparing Quantities - Question 7
Important Questions: Comparing Quantities - Question 8
A person borrowed ₹10,000 at an annual simple interest rate of 8% for 3 years. What is the total amount to be repaid after 3 years?
Detailed Solution for Important Questions: Comparing Quantities - Question 8
Important Questions: Comparing Quantities - Question 9
If a number is increased by 25% and then decreased by 20%, what is the net percentage change?
Detailed Solution for Important Questions: Comparing Quantities - Question 9
Detailed Solution for Important Questions: Comparing Quantities - Question 10
|
76 videos|345 docs|39 tests
|
Information about Important Questions: Comparing Quantities Page
In this test you can find the Exam questions for Important Questions: Comparing Quantities solved & explained in the simplest way possible.
Besides giving Questions and answers for Important Questions: Comparing Quantities, EduRev gives you an ample number of Online tests for practice
|
76 videos|345 docs|39 tests
|
Download as PDF