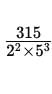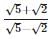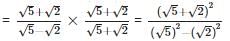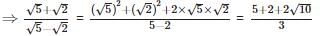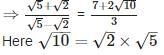RD Sharma Test: Real Numbers - 1 - Class 10 MCQ
25 Questions MCQ Test - RD Sharma Test: Real Numbers - 1
If a is a non-zero rational and √b is irrational, then a√b is:
If HCF(a, b) = 12 and a × b = 1800, then LCM(a, b) is
If the HCF of two numbers is 18 and their LCM is 540, then what is the product of the two numbers?
The number 6n ends with the digit 0 for any natural number n, if and only if:
The smallest number by which 864 must be divided to make it a perfect square is:
The sum of a rational number and an irrational number is always:
The square root of which of the following numbers is rational?
The smallest number by which 392 must be multiplied to get a perfect cube is:
If the LCM of 14 and 35 is 70, what is their HCF?
Which of the following rational numbers has a terminating decimal expansion?
The least positive integer divisible by 20 and 24 is
The HCF of two consecutive odd numbers is always:
If p/q is a rational number and √7 is an irrational number, then p+q√7 is:
The number of irrational numbers between 3 and 4 is:
If ‘a’ and ‘b’ are both positive rational numbers, then
If the LCM of two numbers is 120 and their HCF is 4, which of the following is a possible pair of numbers?
The smallest positive integer that leaves remainders 1, 2, and 3 when divided by 2, 3, and 4 respectively is: