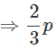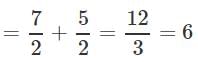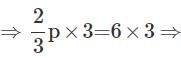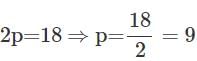Olympiad Test: Algebra - Class 6 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 6 - Olympiad Test: Algebra
Which of the following are used to represent unknown quantities in algebra?
The rule, which gives the number of matchsticks required to make the matchstick pattern L, is
What is the equation for the statement 'half of a number added to 10 is 15'?
Write an equation for the statement 'thrice the length of a room is 340 metres'.
What is the method of finding a solution by trying out various values for the variable called?
A Find the value of 'a' that satisfies the equation 6a = −144.
Choose a value of 'a' that satisfies the equation 6a = -30.
Ramu's father is thrice as old as Ramu. If father's age is 45 years, how old is Ramu?
A number is multiplied by 6 and 12 is added to the product. The result is 84. What is the number?
Find the length of a side of an equilateral triangular garden whose perimeter is 66 m.
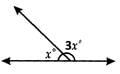
In the given figure, what are the magnitudes of the angles shown?
The length of a rectangle is twice its breadth. If its area is 72 sq. m, find the breadth of the rectangle.
Which of the following is the perimeter of a regular hexagon of side 's' units?
In a piggy bank the number of 25 paise coins is five times the number of 50 paise coins. If there are 120 coins, find the amount in the bank.
|
92 videos|348 docs|54 tests
|




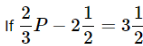 what is the value of p?
what is the value of p?