Olympiad Test: Mensuration - Class 6 MCQ

Perimeter of the rectangle

The perimeter is calculated by adding the lengths of all sides:

• Perimeter = length + breadth + length + breadth
• This simplifies to: Perimeter = 2 × (length + breadth)
• Thus, the formula is: Perimeter = 2(l + b)

The perimeter (P) of a square can be calculated using the formula:

P = 4s

In this formula:

• s represents the length of one side of the square.
• The perimeter is simply four times the length of that side.

For example, if each side of the square measures 1 metre, the perimeter would be:

• P = 4 × 1 m = 4 m

This means that to measure the distance around the square, you would add the lengths of all four sides, which is the same as multiplying the length of one side by four.

• Perimeter of an equilateral triangle: The perimeter of any polygon is the sum of the lengths of all its sides. In an equilateral triangle, all three sides are equal in length.
• Given: The side length of the equilateral triangle is 'a' units.
• Formula for perimeter: Since all sides of an equilateral triangle are equal, the perimeter P can be calculated as P = a + a + a = 3a units
• Therefore, the correct answer is: B: 3a units.

Perimeter:

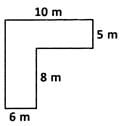
• Definition: The total boundary length of a closed figure is called the perimeter.
• Calculation: To find the perimeter of a closed figure, you simply add up the lengths of all its sides.
• Units: Perimeter is typically measured in units such as inches, feet, meters, etc.
• Importance: Perimeter helps us understand the outer boundary of a shape and is crucial in determining the amount of fencing needed for a garden, the length of a race track, etc.
• Examples: For a square with side length 5 units, the perimeter would be 4 * 5 = 20 units. For a rectangle with lengths 6 units and 4 units, the perimeter would be 2 * (6 + 4) = 20 units.

Surface Area Calculation

• Definition: The amount of surface enclosed by a closed figure is called the area.
• Measurement: Area is measured in square units, such as square metres (m²) or square centimetres (cm²).
• Formula: The formula to calculate the area varies by shape:
  • For a square: Area = side × side
  • For a circle: Area = π × radius²
• Importance: Knowing the surface area is essential in fields like construction, architecture, and geometry.
• Applications: Area calculations help determine the material needed to cover surfaces, assess land area, and solve practical problems.

Solution:

The perimeter of a rectangle can be calculated using the formula:

• Perimeter = 2 × (length + breadth)

Given:

• Perimeter = 170 m
• Length = 50 m

Substituting the known values into the formula:

• 2 × (50 + breadth) = 170
• 50 + breadth = 170 / 2
• 50 + breadth = 85
• breadth = 85 - 50
• breadth = 35 m

Thus, the breadth of the rectangle is 35 m.

To find the length of a rectangle given its area and breadth:

The formula for the area of a rectangle is:

• Area = Length × Breadth

Given:

• Area = 630 sq. cm
• Breadth = 15 cm

To find the length:

• Rearranging the formula gives:
• Length = Area / Breadth
• Substituting the values:
• Length = 630 / 15
• Calculating:
• Length = 42 cm

Thus, the length of the rectangle is 42 cm.

Solution:

The perimeter of the plot can be calculated using the formula:

• Perimeter = 2 × (length + breadth)
• Here, length = 30 m and breadth = 15 m.
• So, Perimeter = 2 × (30 m + 15 m) = 2 × 45 m = 90 m.

Next, we determine the number of stones needed:

• The distance between each stone is 10 m.
• To find the number of stones, divide the perimeter by the distance between stones:
• Number of stones = 90 m / 10 m = 9.

Thus, Samuel needs a total of 9 stones.

We know that,

Area=l∗b

l=3.2m
b=1.5m
l×b=3.2×1.5 =4.80 sq m
to apply point - first count the no of digit after decimal in the numbers
like here one here in 3.2 and one in 1.5 so a total of 2
now apply decimal from back to 2 decimal place

Solution:

The perimeter of the garden can be calculated based on the total length covered by the students. Here’s how:

• Each student covers a length of 1.75 m.
• There are 80 students standing in line.
• The total length covered by the students is:
• 80 × 1.75 m = 140 m

Thus, the perimeter of the garden is 140 m.

Solution:

The area of one square is calculated using the formula:

• Area of square = side × side
• For a square with a side of 3 cm:
• Area = 3 cm × 3 cm = 9 sq. cm

To find the total area of the table top covered by 25 squares:

• Total area = number of squares × area of one square
• Total area = 25 × 9 sq. cm
• Total area = 225 sq. cm

Solution:

• Length of the rectangular plot: 900 m
• Breadth of the rectangular plot: 700 m
• Calculate the perimeter:
• Perimeter = 2 × (Length + Breadth)
• Perimeter = 2 × (900 m + 700 m) = 2 × 1600 m = 3200 m
• For three rounds of fencing:
• Total perimeter for 3 rounds = 3 × 3200 m = 9600 m
• Calculate the total cost:
• Cost per metre = Rs. 8
• Total amount spent = 9600 m × Rs. 8 = Rs. 76,800

1 sq. m = 10,000 sq. cm

Solution:

To find the area occupied by five wooden planks, follow these steps:

• Length of one plank: 6 m
• Breadth of one plank: 3 m
• Area of one plank = Length × Breadth = 6 m × 3 m = 18 sq. m
• Number of planks: 5
• Total Area of 5 planks = 18 sq. m × 5 = 90 sq. m

The area occupied by the five wooden planks is 90 sq. m.

Solution:

• Area of the poster: 2.5 m × 2.5 m = 6.25 sq. m
• Area of the wall: 10.5 m × 8.5 m = 89.25 sq. m
• Area to be painted: 89.25 sq. m - 6.25 sq. m = 83.00 sq. m
• Cost of painting: 83 sq. m × Rs. 12 = Rs. 996

10×5 = 50sq.m 
6×8 = 48 sq. m 
∴ The required area = 50 + 48 = 98 sq. m

Area of the pond:

• Dimensions: 3 m × 2 m
• Area = 6 sq m

Area of the park:

• Side length: 28 m
• Area = 28 m × 28 m = 784 sq m

Area of the park excluding the pond:

• Area = 784 sq m - 6 sq m
• Result = 778 sq m

Explanation:

• Given: An isosceles triangle with equal sides of length p units and an unequal side of length q units.
• Perimeter of a triangle: The perimeter of a triangle is the sum of the lengths of its three sides.
• For an isosceles triangle: In an isosceles triangle, two sides are equal in length and one side is unequal.
• Perimeter of the isosceles triangle: To find the perimeter of the isosceles triangle, we add the lengths of the three sides, which are p, p, and q.
• Perimeter = p + p + q = 2p + q

Therefore, the correct answer is:
Answer: B

Explanation:

• Given: Let the length of the rectangle be L and the breadth be B.
• Twice the sum of length and breadth: 2(L + B)
• Resultant of twice the sum of length and breadth: This is the perimeter of the rectangle, which is given by 2(L + B).
• Therefore, the correct answer is option B: Its perimeter.

Steps to find the measure of the side of the square:

• Perimeter of a square: The perimeter is the total length around the square, which is the sum of all four sides.
• Given information: The perimeter of the square is 728 cm.
• Formula: Let the side of the square be x. Thus, the perimeter can be expressed as 4x.
• Equation: Set up the equation: 4x = 728.
• Solve for x: Divide both sides by 4: x = 728 / 4 = 182.

Conclusion:

• Measure of the side: The side of the square is 182 cm.
• By following the steps outlined, you can easily determine the side length of the square.