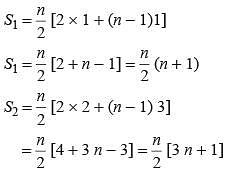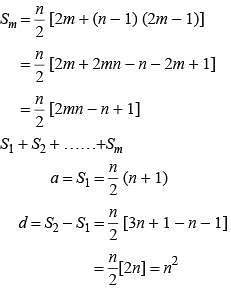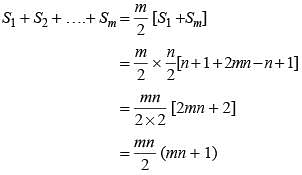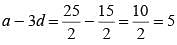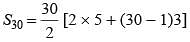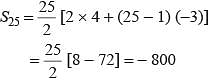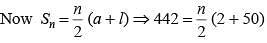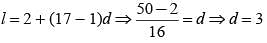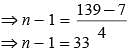Math Olympiad Test: Arithmetic Progression- 1 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Arithmetic Progression- 1
If S1, S2, S3, …. Sm are the sum of n terms of m arithmetic progression whose first terms are 1, 2, 3, …. m and common differences are 1, 3, 5, … (2m - 1) respectively. What is the value of S1 + S2 + …. Sm?
If the 3rd and 7th terms of an arithmetic progression are 17 and 27 respectively. Find the first term of arithmetic progression.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If four numbers in arithmetic progression are such that their sum is 50 and the greatest number is 4 times the least. Which number is the least one?
If 8th term of an arithmetic progression is 31 and its 15th term is 16 more than 11th term of the arithmetic progression. What is the first term of that arithmetic progression?
What is the sum of first 30 terms of the arithmetic progression whose 2nd term is 8 and 4th term is 14?
Find the sum of first 25 terms of an arithmetic progression whose nth term is given by 7 - 3n.
The first term of an arithmetic progression is 2 and the last term is 50. The sum of all these terms is 442. What is the common difference?
The sum of the three numbers in arithmetic progression is 12. The sum of their cubes is 288. What are the numbers?
If the sum of n terms of an Arithmetic Progression is given by Sn = 3n2 + 2n. Find its first term and common difference.
How many terms are there in the Arithmetic Progression?
7, 11, 15, …..139?
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|