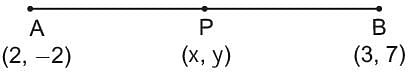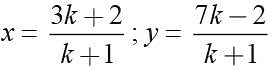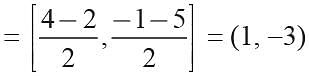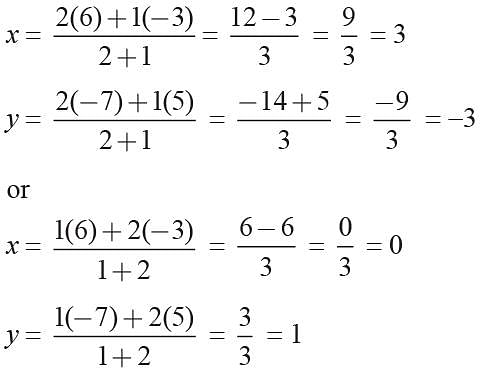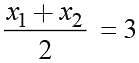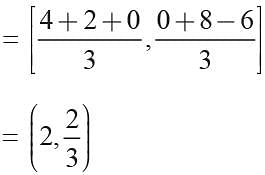Math Olympiad Test: Coordinate Geometry- 1 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Coordinate Geometry- 1
Find the value of k for which the points A (3, 2), B (4, k) and C (5, 3) are collinear.
Find ratio in which the line 2x + y - 4 = 0 divides the line segment joining A(2, -2) and B(3, 7).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The co-ordinates of ends of a diameter of a circle are (4, -1) and (-2, -5). Find the centre of the circle.
The area of a triangle with vertices (a, b + c) and (b, c + a) and (c, b + a) is
Find the co-ordinates of the points which trisects the line joining (-3, 5) and (6, -7).
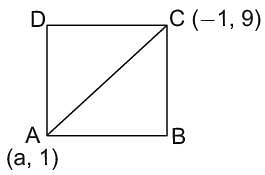
The ends of a diagonal of a square have the coordinates (a, 1) and (-1, a), find a if the area of the square is 50 square units.
Two vertices of a triangle are (2, -4) and (1, 3). If the origin is the centroid of the triangle then what is the third vertex?
What is the locus of a point equidistant from the point (2, 4) and y-axis?
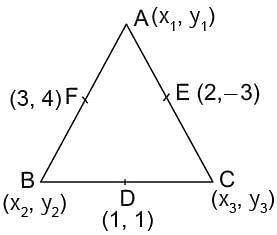
If the coordinates of the mid-point of the sides of a triangle are (1, 1) (2, -3), and (3, 4) what is the centroid?
What is the value of k, so that the points A(8, 1), B(3, -4), and C(2, K) are collinear?
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|