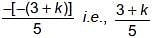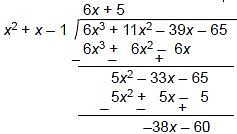Math Olympiad Test: Polynomials - 3 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Polynomials - 3
If sum of all zeros of the polynomial 5x2 – (3 + k)x + 7 is zero, then zeroes of the polynomial 2x2 – 2(k + 11)x + 30 are
px3 + qx2 + rx + s = 0 is said to be cubic polynomial, if _______.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a and b are the roots of the quadratic equation x2 + px + 12 = 0 with the condition a – b = 1, then the value of ‘p’ is _______.
If the sum of the product of the zeroes taken two at a time of the polynomial f(x) = 2x3 – 3x2 + 4tx – 5 is –8, then the value of t is _______.
A cubic polynomial with sum of its zeroes, sum of the product of its zeroes taken two at a time and the product of its zeroes as –3, 8, 4 respectively, is _______.
What will be the value of p(3), if 3 is one of zeroes of polynomial p(x) = x3 + bx + D?
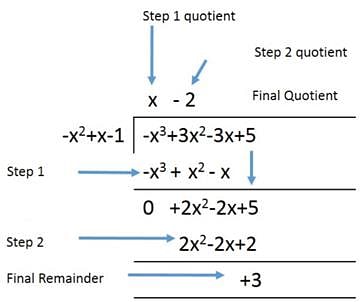
When x3 – 3x2 + 3x + 5 is divided by x2 – x + 1, the quotient and remainder are _______.
If p, q are the zeroes of the polynomial f(x) = x2 + k(x – 1) – c, then (p – 1)(q – 1) is equal to _______.
Which of the following graph has more than three distinct real roots?
What should be subtracted from f (x) = 6x3 + 11x2 – 39x – 65 so that f(x) is exactly divisible by x2 + x – 1?
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|