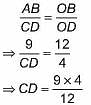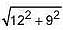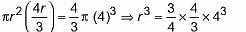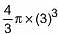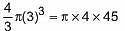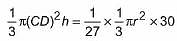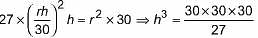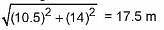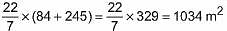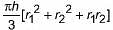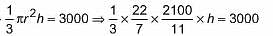Math Olympiad Test: Surface Area and Volume- 3 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Surface Area and Volume- 3
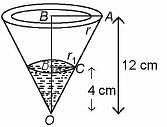
An inverted cone of vertical height 12 cm and the radius of base 9 cm contains water to a depth of 4 cm. Find the area of the interior surface of the cone not in contact with the water. [Use π = 22/7]
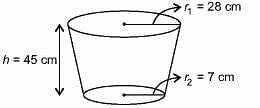
If the radii of the circular ends of bucket in the form of frustum are 28 cm and 7 cm and the height is 45 cm. The capacity of the bucket is _____.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cylinder, whose height is two-thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is ____.
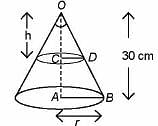
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 1/27 of the volume of the given cone, at what height above the base is the section made?
Study the question and the statements given below and decide which of the statement(s) is/are necessary to answer the question.
What is the capacity of the cylindrical tank?
I. The area of the base is 61,600 sq. cm.
II. The height of the tank is 1.5 times the radius.
III. The circumference of base is 880 cm.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r.
A tent is in the shape of a right circular cylinder up to a height of 3 m and then becomes a right circular cone with a maximum height of 13.5 m above the ground. Calculate the cost of painting the inner side of the tent at the rate of ₹ 2 per m2, if the radius of the base is 14 m.
A bucket is in the form of a frustum of a cone, its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm respectively. How many litres can the bucket hold?
In a marriage ceremony of her daughter Poonam, Ashok has to make arrangements for the accommodation of 150 persons. For this purpose, he plans to build a conical tent in such a way that each person have 4 sq. metres of the space on ground and 20 cubic metres of air to breath. What should be the height of the conical tent?
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|