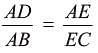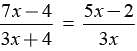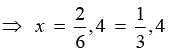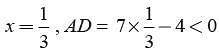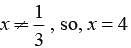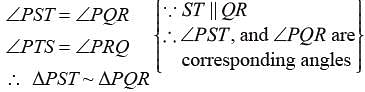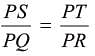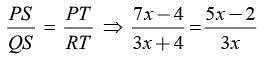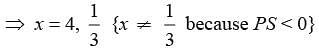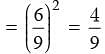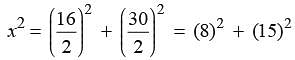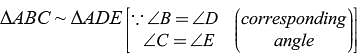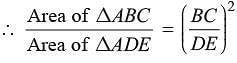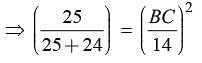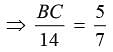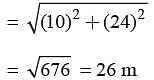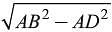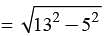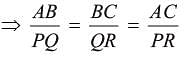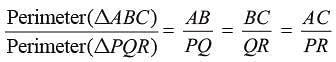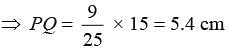Math Olympiad Test: Triangles - 2 - Class 10 MCQ
15 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Triangles - 2
In an isosceles triangle AB = AC = 25 cm BC = 14 cm. What is the length of altitude from A on BC?
The area of two equilateral triangle are in the ratio 196 : 169. What is the ratio between their perimeters?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
D and E are points on the sides AB and AC respectively of a DABC such that DE || BC find value of x if AD = (7x - 4) cm, AE = (5x - 2) cm, DB = (3x - 4) cm, EC = 3x cm
In the given figure in DPQR, ST || QR, so that PS = (7x - 4) cm, PT = (5x - 2) cm, QS = (3x + 4) cm, RT = 3x cm.
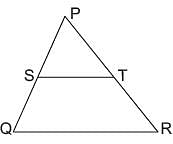
What is the value of x?
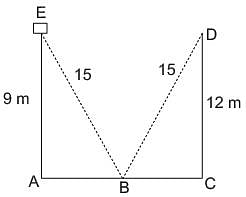
A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. What is the width of the street?
The corresponding altitude of two similar triangle are 6 cm and 9 cm respectively. What is ratio of their areas?
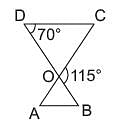
In the given figure, ΔODC ~ ΔOBA, ∠BOC = 115°, ∠CDO = 70°. What is the value of ∠OAB?
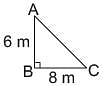
A tree is broken of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. What is the original height of the tree?
An exterior angle of a triangle measures 110° and its interior opposite angles are in the ratio 2 : 3. Which is the largest angle of the triangle?
What is the perimeter of a rhombus the length of whose diagonal are 16 cm and 30 cm?
In the given figure BC is parallel to DE. Area of DABC is 25 cm2. Area of trapezium BCED is 24 cm2, if DE = 14 cm
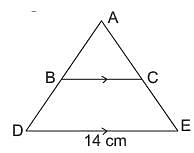
What is the length of BC?
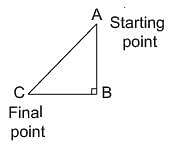
A man goes 10 m due south and then 24 m due west. How far is he from the starting point?
A vertical pole 12 m long casts a shadow of 8 m long on the ground. At the same time, a tower casts the shadow 40 m long on the ground. What is the height of the tower?
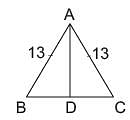
In an isosceles triangle ΔABC if AB = AC = 13 cm and altitude from A on BC is 5 cm. What is the length of BC?
The Perimeter of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm. Then what is the corresponding side of the second circle?
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|


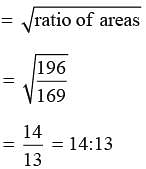
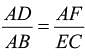
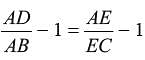
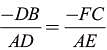 adjusting this expression, we have
adjusting this expression, we have