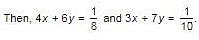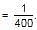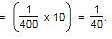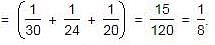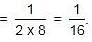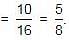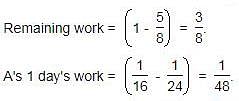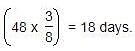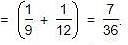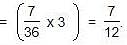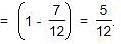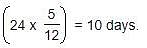Test: Arun Sharma Based Level 3: Time & Work - CUET Commerce MCQ
30 Questions MCQ Test General Test Preparation for CUET - Test: Arun Sharma Based Level 3: Time & Work
A can do a work in 15 days and B in 20 days. If they work on it together for 4 days, then the fraction of the work that is left is :
A can lay railway track between two given stations in 16 days and B can do the same job in 12 days. With help of C, they did the job in 4 days only. Then, C alone can do the job in:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A, B and C can do a piece of work in 20, 30 and 60 days respectively. In how many days can A do the work if he is assisted by B and C on every third day?
A is thrice as good as workman as B and therefore is able to finish a job in 60 days less than B. Working together, they can do it in:
A alone can do a piece of work in 6 days and B alone in 8 days. A and B undertook to do it for Rs. 3200. With the help of C, they completed the work in 3 days. How much is to be paid to C?
If 6 men and 8 boys can do a piece of work in 10 days while 26 men and 48 boys can do the same in 2 days, the time taken by 15 men and 20 boys in doing the same type of work will be:
A can do a piece of work in 4 hours; B and C together can do it in 3 hours, while A and C together can do it in 2 hours. How long will B alone take to do it?
A can do a certain work in the same time in which B and C together can do it. If A and B together could do it in 10 days and C alone in 50 days, then B alone could do it in:
A does 80% of a work in 20 days. He then calls in B and they together finish the remaining work in 3 days. How long B alone would take to do the whole work?
A machine P can print one lakh books in 8 hours, machine Q can print the same number of books in 10 hours while machine R can print them in 12 hours. All the machines are started at 9 A.M. while machine P is closed at 11 A.M. and the remaining two machines complete work. Approximately at what time will the work (to print one lakh books) be finished ?
A can finish a work in 18 days and B can do the same work in 15 days. B worked for 10 days and left the job. In how many days, A alone can finish the remaining work?
4 men and 6 women can complete a work in 8 days, while 3 men and 7 women can complete it in 10 days. In how many days will 10 women complete it?
A and B can together finish a work 30 days. They worked together for 20 days and then B left. After another 20 days, A finished the remaining work. In how many days A alone can finish the work?
P can complete a work in 12 days working 8 hours a day. Q can complete the same work in 8 days working 10 hours a day. If both P and Q work together, working 8 hours a day, in how many days can they complete the work?
10 women can complete a work in 7 days and 10 children take 14 days to complete the work. How many days will 5 women and 10 children take to complete the work?
X and Y can do a piece of work in 20 days and 12 days respectively. X started the work alone and then after 4 days Y joined him till the completion of the work. How long did the work last?
A is 30% more efficient than B. How much time will they, working together, take to complete a job which A alone could have done in 23 days?
Ravi and Kumar are working on an assignment. Ravi takes 6 hours to type 32 pages on a computer, while Kumar takes 5 hours to type 40 pages. How much time will they take, working together on two different computers to type an assignment of 110 pages?
A, B and C can complete a piece of work in 24, 6 and 12 days respectively. Working together, they will complete the same work in:
Sakshi can do a piece of work in 20 days. Tanya is 25% more efficient than Sakshi. The number of days taken by Tanya to do the same piece of work is:
A takes twice as much time as B or thrice as much time as C to finish a piece of work. Working together, they can finish the work in 2 days. B can do the work alone in:
A and B can complete a work in 15 days and 10 days respectively. They started doing the work together but after 2 days B had to leave and A alone completed the remaining work. The whole work was completed in :
A and B can do a piece of work in 30 days, while B and C can do the same work in 24 days and C and A in 20 days. They all work together for 10 days when B and C leave. How many days more will A take to finish the work?
A works twice as fast as B. If B can complete a work in 12 days independently, the number of days in which A and B can together finish the work in
Twenty women can do a work in sixteen days. Sixteen men can complete the same work in fifteen days. What is the ratio between the capacity of a man and a woman?
A and B can do a work in 8 days, B and C can do the same work in 12 days. A, B and C together can finish it in 6 days. A and C together will do it in :
A can finish a work in 24 days, B in 9 days and C in 12 days. B and C start the work but are forced to leave after 3 days. The remaining work was done by A in:
X can do a piece of work in 40 days. He works at it for 8 days and then Y finished it in 16 days. How long will they together take to complete the work?
If A and B together can complete a piece of work in 15 days and B alone in 20 days, in how many days can A alone complete the work?
A and B together can do a piece of work in 30 days. A having worked for 16 days, B finishes the remaining work alone in 44 days. In how many days shall B finish the whole work alone?
|
154 videos|396 docs|723 tests
|
|
154 videos|396 docs|723 tests
|