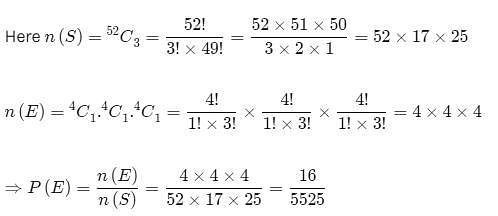Test: Probability- 4 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - Test: Probability- 4
A bag contains four black and five red balls. If three balls from the bag are chosen at random, what is the chance that they are all black?
From a pack of 52 playing cards, three cards are drawn at random. Find the probability of drawing a king, a queen and jack.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A group of investigators took a fair sample of 1972 children from the general population and found that there are 1000 boys and 972 girls. If the investigators claim that their research is so accurate that the sex of a new bom child can be predicted based on the ratio of the sample of the population, then what is the expectation in terms of the probability that a new child bom will be a girl?
A bag contains 6 red, 4 white and 8 blue balls. If three balls are drawn at random, find the probability that (i) all the three balls are of the same colour.
A and B are two candidates seeking admission to the IIMs. The probability that A is selected is 0.5 and the probability that both A and B are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9.
The odds in favour of standing first of three students Amit, Vikas and Vivek appearing at an examination are 1 : 2. 2 : 5 and 1 : 7 respectively. What is the probability that either of them will stand first (assume that a tie for the first place is not possible).
A and B are two mutually exclusive events of an experiment. If P(A') = 0.65, P(A u B) = 0.65 and P(B) = p , find the value o f p.
The odds against an event is 5 : 3 and the odds in favour of another independent event is 7 : 5. Find the probability that at least one of the two events will occur.
A husband and a wife appear in an interview for two vacancies for the same post. The probability of husband’s selection is (1/7) and that of the wife’s selection is 1/5. What is the probability that (i) both of them will be selected?
There are two bags, one of them contains 5 red and 7 white balls and the other 3 red and 12 white balls, and a ball is to be drawn from one or the other of the two bags. Find the chance of drawing a red ball.
Two fairdices are thrown. Giventh at the sum of the dice is less than or equal to 4, find the probability that only one dice shows two.
If 8 coins are tossed, what is the chance that one and only one will turn up Head?
Out of all the 2 - digit integers between 1 to 200, a 2-digit number has to be selected at random. What is the probability that the selected number is not divisible by 7?
Tom and Dick are running in the same race; the probability of their winning are 1/5 and 1/2 respectively . Find the probability that (i) either of them will win the race.
Amamath appears in an exam that has 4 subjects. The chance he passes an individual subject’s test is 0.8. What is the probability that he will (i) pass in all the subjects?
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|