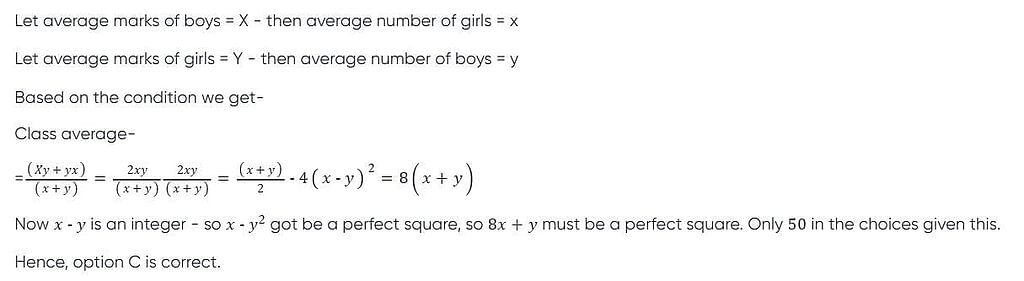Arun Sharma Test: Averages- 3 - CAT MCQ
15 Questions MCQ Test Quantitative Aptitude (Quant) - Arun Sharma Test: Averages- 3
The average marks of the girls in a class is equal to the number of boys and the average marks of boys is equal to the number of girls. If the class average is 4 less than the average of both the boys’ and the girls’ average marks, what will be the number of students in the class?
A, B, C, D and E are five consecutive integers and the average of these five numbers is less than 1/4th of A. Then A is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Ram was born 30 years after his father was born and Ram's sister was born 25 years after Ram’s mother was born. The average age of the Ram family is 26.25 years right now. Ram's sister will get married 4 years from now and will leave the family. Then the sum of age of the family will be 107 years. What is the age of Ram's father?
India is supposed to send its boxing team for Olympics in each of the following 10 weight group divisions.
A (48 kg -52 kg) B (52 kg - 56 kg)
C (56 k g - 60 kg) D (60 k g - 64 kg)
E (64 kg -68 kg) F (68 kg - 72 kg)
G (72 k g - 76 kg) H (76 k g - 80 kg)
I (80 kg - 84 kg) J (84 kg - 88 kg)
After selecting one player from each group, their average weight comes out to be 68 kg. if one of the players named X leaves
If X leaves the team, and two new players join the group, then their average weight increases to 68 kg. These players can be from group....
In continuation with previous question, the average of all the groups together, which group contributes most in overall average?
The average age of Mr and Mrs Sinha at the time of their marriage in 1972 was 23 years. On the occasion of their anniversary in 1976, they observed that the average age of their family had come down by 4 years compared to their average age at the time of their marriage. This was due to the fact that their son Vicky was born during that period. What was the age of Vicky in 1980?
Sachin Tendulkar has a certain batting average N (a whole number) in his career of 86 innings. In the 87th inning, he gets out after scoring 270 runs which increases his batting average by a whole number. The batting average is calculated by dividing the total number of runs scored by the total number of innings played by the player. How many values of his new average is/are possible?
Read the passage below and solve the questions based on it.
The average score of a batsman for a certain number of innings was 21 75 per inning. He played 3 innings more and scored 28. 34 and 37 runs respectively, thus increasing his average by 1.125.
Q. How many innings in all did he play?
Manu earns ₹4000 per month and wants to save an average of ₹550 per month in a year. In the first nine months, his monthly expense was ₹3500, and he foresees that, tenth month onward, his monthly expense will increase to ₹3700. In order to meet his yearly savings target, his monthly earnings, in rupees, from the tenth month onward should be
The average of three integers is 13. When a natural number n is included, the average of these four integers remains an odd integer. The minimum possible value of n is
Mukul has earned as an average of 4,200 dollars for the first eleven months of the year. If he justifies his staying in the US on the basis of his ability to earn at least 5000 dollars per month for the entire year, then how much should he earn (in dollars) in the last month to achieve his required average for the whole year?
The average of the 5 consecutive even numbers A,B,C,D ,E is 52.what is the product of B & E
If the average marks of 17 students in a class is A. The marks of the students when arranged in either an ascending or a descending order was found to be in arithmetic progression. The class teacher found that the students who were ranked 3rd, 7th, 9th, 11th, 15 th had copied in the exam and hence got all of them rusticated. The average of the remainder of the class was B. Then
The average salary of 30 officers in a firm is Rs.120 and the average salary of laborers is Rs. 40. Find the total number of laborers if the average salary of the firm is Rs. 50.
We write down all the digits from 1-9 side by side. Now. we put "+" between as many digits as we wish to. so that the sum of numbers become 666.It is explained below: 1 2 3 4 5 6 7 8 9 = 666`
Now suppose we put plus signs al following places: 12 + 3 5 + 67 + 89 = 513` Since there are four numbers, so the average can be calculated by dividing the bum by 4. What is the average if the sum is 666?
In the above question, what is the average if the sum is 261?
|
196 videos|131 docs|110 tests
|
|
196 videos|131 docs|110 tests
|