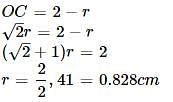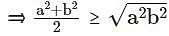Test: Geometry- 2 - CAT MCQ

PQRS is a Trapezzium, in which PQ is Parralel to RS, and PQ = 3 (RS) . The diagnol of the Trapezzium intersect each other at X, then the ratio of,  ar ( ∆ PXQ)  : ar ( ∆ RXS)  is?

Let ABCDEF be a regular hexagon. What is the ratio of the area of the triangle ACE to that of the hexagon ABCDEF?

A pond 100 m in diameter is surrounded by a circular grass walk-way 2 m wide. How many square metres of grass is the on the walk-way?

The dimensions of a rectangular box are in the ratio of 1:2:4 and the difference between the costs of covering it with the cloth and a sheet at the rate of Rs 20 and Rs 20.5 per sq m respectively is Rs 126. Find the dimensions of the box.

The ratio of the area of a square inscribed in a semicircle to that of the area of a square inscribed in the circle of the same radius is

The ratio of the area of a square to that of the square drawn on the its the diagonal is

What is the area of the triangle in which two of its medians 9 cm and 12 cm long intersect at the right angles?

Four horses are tethered at four comers of a square plot of side 14 m so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. Find the ungrazed area.

Two sides of a triangle are 4 and 5. Then, for the area of the triangle, which one of the following bounds is the sharpest?

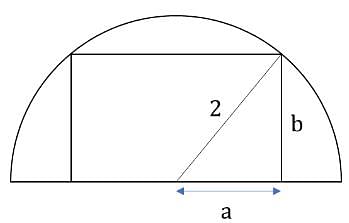
A rectangle with the largest possible area is drawn inside a semicircle of radius 2 cm. Then, the ratio of the lengths of the largest to the smallest side of this rectangle is?

The lengths of all four sides of a quadrilateral are integer valued. If three of its sides are of length 1 cm, 2 cm and 4 cm, then the total number of possible lengths of the fourth side is

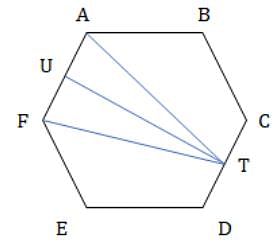
Suppose the length of each side of a regular hexagon ABCDEF is 2 cm. If T is the mid point of CD, then the length of AT, in cm, is